Amplitude Transduction

This post is part of the Q# Holiday Calendar 2022. Check out the calendar for more great posts !

Digital encoding and amplitude encoding

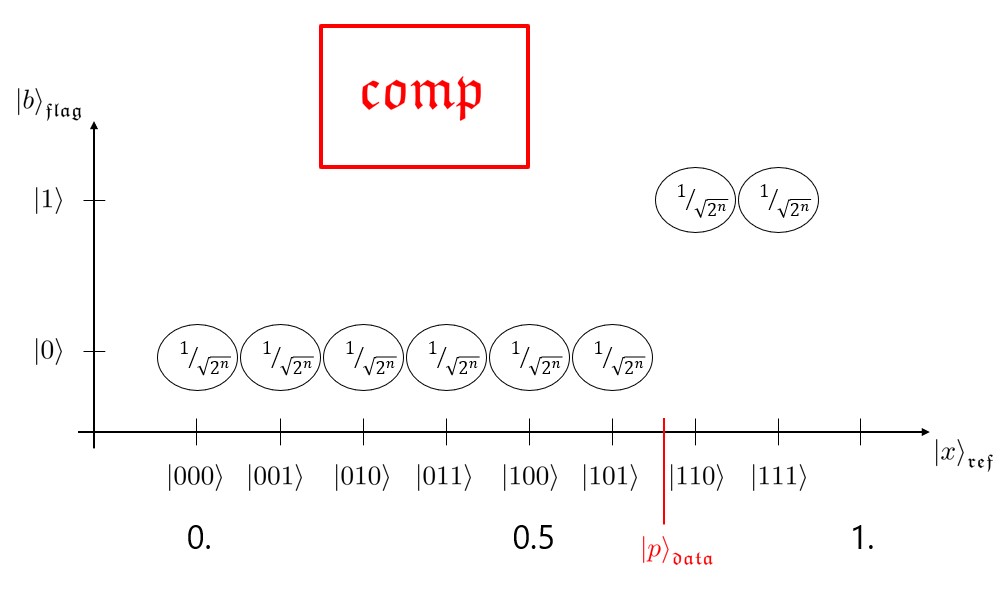
A vector \(x = (x_i)_{1 \leq i \leq N}\) can be represented by at least two different quantum states: the digital encoding and the amplitude encoding quantum states.

\[\vert \text{digital encoding} \rangle = \frac{1}{\sqrt{N}} \sum_{i=1}^N \vert i \rangle_I \vert x_i^{(b)} \rangle_D.\] \[\vert \text{amplitude encoding} \rangle = \frac{1}{\vert\vert x \vert\vert_2} \sum_{i=1}^N x_i \vert i \rangle_I.\]

In both cases, the index register \(\vert \,\,\, \rangle_I\) has length \(\log_2 (N)\) where \(N\) is the dimension of the vector \(x\). The digital encoding state also needs a data register \(\vert \,\,\, \rangle_D\) that contains a binary representation \(x_i^{(b)}\) of \(x_i\). The length of the data register is given by number of bits of the binary representation \(x_i^{(b)}\). \(\frac{1}{\sqrt{N}}\) and \(\frac{1}{\vert\vert x \vert\vert_2}\) are normalization constants: \(\vert\vert x \vert\vert_2 =\sqrt{ \sum_{i=1}^N \vert x_i \vert^2 }\).

The amplitude encoding state is more memory efficient: it needs a smaller number of qubits. The digital encoding state is usually easier to prepare and to process. It is indeed straightforward to translate a classical algorithm that computes a function \(f\) into a quantum algorithm that transforms the digital encoding of \(x = (x_i)_{1 \leq i \leq N}\) into the digital encoding of \(f(x) = (f(x_i))_{1 \leq i \leq N}\):

\[\frac{1}{\sqrt{N}} \sum_{i=1}^N \vert i \rangle_I \vert x_i^{(b)} \rangle_D \mapsto \frac{1}{\sqrt{N}} \sum_{i=1}^N \vert i \rangle_I \vert f(x_i^{(b)}) \rangle_D.\]

Both encodings are superpositions over the index register \(\vert \,\,\, \rangle_I\). In digital encoding, the superposition is uniform and the data \(x_i\) is stored in a second register. In amplitude encoding, the data is the probability amplitude.

Amplitude transduction: definition

It is sometimes necessary to convert between digital and amplitude encodings. Black-box quantum state preparation without arithmetic describes an efficient algorithm to convert a digital encoding into an amplitude encoding. This quantum algorithm is called amplitude transduction.

More precisely, given access to a quantum operation \(O_D^{(x)}\) that prepares a digital encoding of \(x\), amplitude transduction constructs the quantum operation \(O_A^{(x)}\) that prepares an amplitude encoding of \(x\).

\[O_D^{(x)} \vert i \rangle_I \vert 0 \rangle_D = \vert i \rangle_I \vert x_i \rangle_D.\] \[O_A^{(x)} \vert 0 \rangle_I = \frac{1}{\vert\vert x \vert\vert_2} \sum_{i=1}^N x_i \vert i \rangle_I.\]

Amplitude transduction: use cases

A close cousin of amplitude encoding is probability encoding:

\[\vert \text{probability encoding} \rangle = \frac{1}{\vert\vert x \vert\vert_1} \sum_{i=1}^N \sqrt{x_i} \vert i \rangle_I.\]

Black-box quantum state preparation without arithmetic also describes an efficient algorithm to convert a digital encoding into a probability encoding.

When the probability encoding state is measured in the computational basis, the outcome is \(i\) with probability proportional to \(\vert x_i \vert\). Therefore probability encoding is useful for applications where the probability distribution proportional to \((\vert x_i \vert)_{1 \leq i \leq N}\) is sampled. This includes discrete-time quantum walks and the linear combination of unitaries (LCU) technique.

Probability or amplitude encodings are also used for instance in quantum algorithms that solve linear system of equations.

Amplitude transduction: Q# implementation

Here is a Q# implementation of the variant of amplitude transduction that prepares a probability encoding assuming access to \(O_D^{(x)}\), the quantum operation that prepares a digital encoding of \(x\).

It leverages functions and operations of the Amplitude Amplification namespace of the Q# standard library for fixed point amplitude amplification.

It also uses the Quantum Numerics library to work with quantum digital encodings of real values: the quantum version of floats.