Estimation de phase : forces et faiblesses des variantes

L’estimation de phase est un algorithme quantique permettant de calculer la valeur propre d’une opération quantique \(U\) associée à un état quantique \(\vert \psi \rangle\). On suppose qu’on sait implémenter \(U\) et que l’état \(\vert \psi \rangle\) est disponible en mémoire quantique. En revanche on ne connait pas la valeur propre \(\phi\) et on cherche à la calculer. Comme ce calcul est fait avec une précision qui n’est pas infinie, on parle d’estimation. Comme la valeur propre est d’abord enregistrée sous la forme \(e^{i \phi}\), on parle d’estimation de phase.

Il existe de nombreuses variantes de l’algorithme quantique d’estimation de phase. Dans cet article, nous allons passer en revue quelques variantes et en donner les forces et faiblesses.

L’estimation quantique de phase

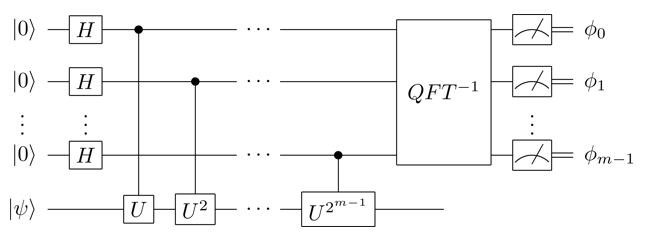
L’estimation quantique de phase écrit la phase \(\phi\) dans un registre quantique. C’est sans doute la variante la plus connue de l’estimation de phase. Elle utilise une transformée de Fourier inverse pour que la phase soit retranscrite en binaire. Elle requiert \(m\) qubits auxiliaires, où \(m\) est le nombre de bits de précision avec lequel on cherche à calculer \(\phi\). Une fois mesuré, chacun des \(m\) qubits auxiliaires fournit un bit de la phase \(\phi\) recherchée.

Tout l’algorithme est réalisé par un seul circuit quantique, assez long. Cela suppose donc que le hardware quantique disponible soit suffisamment performant, en nombre de qubits et en fidélité des portes quantiques appliquées.

L’avantage de l’estimation quantique par rapport aux versions itératives dont nous allons parler ensuite est que la phase estimée est disponible en mémoire quantique si on ne réalise pas les \(m\) mesures finales. La phase calculée peut donc directement servir d’input à un autre algorithme quantique.

Par exemple, les premières versions de l’algorithme HHL, qui permet de résoudre un système linéaire, consistait à calculer par estimation quantique de phase les valeurs propres de la matrice à inverser. Il était important de garder ces valeurs en mémoire quantique pour ensuite pouvoir toutes les inverser en superposition. Pour clore cette disgression sur HHL, notez qu’on connait aujourd’hui des méthodes plus directes comme la qubitisation et le traitement quantique du signal.

L’implémentation Q# de l’estimation quantique de phase fait partie de la bibliothèque standard Q#. La concision de cette implémentation peut surprendre, étant donné le rôle central de l’estimation de phase en algorithmique quantique.

L’estimation itérative de phase

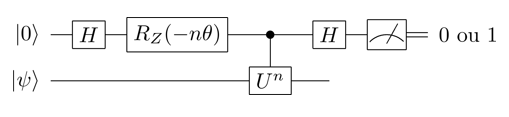
L’estimation itérative de phase décompose le gros circuit de l’estimation quantique de phase en plusieurs circuits de plus petite taille et délègue la partie du calcul assurée par la transformée de Fourier quantique inverse à un processeur classique. Chaque itération consiste à exécuter le circuit suivant :

On peut se convaincre en faisant les calculs que les probabilités respectives de mesurer \(0\) et \(1\) pour le qubit du haut sont :

\[\Pr(0) = \cos^2 (n \frac {\phi - \theta} {2}).\] \[\Pr(1) = \sin^2 (n \frac {\phi - \theta} {2}).\]

Chaque exécution de ce circuit apporte donc un peu d’information sur \(\phi\), la phase qu’on cherche à calculer.

Ce circuit est plus court que celui de l’estimation quantique de phase : il n’utilise qu’un qubit auxiliaire, qu’une seule itérée de \(U\) (i.e. \(U^n\)) et pas de transformée de Fourier. En revanche on va devoir l’exécuter plusieurs fois, avec différentes valeurs de \(\theta\) et \(n\).

Selon la façon dont sont choisis les paramètres \(\theta\) et \(n\), on donne différents noms à l’estimation itérative de phase. Intéressons-nous maintenant en détail à trois de ces variantes :

• L’estimation Bayésienne de phase.
• L’estimation robuste de phase.
• L’estimation de phase par marche aléatoire.

L’estimation Bayésienne de phase

On fixe tout d’abord le nombre de bits avec lesquel on cherche à décrire la phase \(\phi\) recherchée. Pour \(m\) bits de précision sur \(\phi\), il y a donc \(2^m\) valeurs envisagées pour \(\phi\).

On choisit une distribution a priori pour \(\phi\). On peut par exemple prendre la distribution uniforme. On affecte dans ce cas la probabilité \(\frac{1}{2^m}\) à chacune des \(2^m\) valeurs envisagées pour \(\phi\) :

\[\Pr(\phi_a) = \frac{1}{2^m} .\]

A chaque itération, on mesure le qubit du haut du circuit de l’estimation itérative de phase et on obtient un résultat de mesure, qu’on note \(d\) et qui peut valoir \(0\) ou \(1\). Pour chacune des \(2^m\) valeurs envisagées pour \(\phi_a\), on calcule la vraisemblance d’avoir mesuré \(d\) si la vraie valeur de \(\phi\) était \(\phi_a\). D’après le circuit de l’estimation itérative de phase, ce calcul consiste à évaluer la formule suivante :

\[\Pr(d | \phi_a) = \cos^2 (n \frac {\phi_a - \theta} {2} + d \frac{\pi}{2}) .\]

On met alors à jour la distribution qui représente notre connaissance de \(\phi\) en suivant la formule de Bayes. Pour chacune des \(2^m\) valeurs envisagées pour \(\phi\) :

\[\Pr(\phi_a | d) = \frac {\Pr(d | \phi_a) \Pr(\phi_a)} {\Pr(d)} .\]

La seule grandeur qu’on n’a pas déjà calculée est \(\Pr(d)\). On obtient sa valeur par normalisation, c’est-à-dire en observant que la somme sur \(a\) des \(\Pr(\phi_a \vert d)\) vaut 1 :

\[\Pr(d) = \sum_{a=1}^{2^m} \Pr(d | \phi_a) \Pr(\phi_a) .\]

La distribution a posteriori devient la distribution a priori de la prochaine itération. Dit autrement, on remplace chacune des \(2^m\) grandeurs \(\Pr(\phi_a)\) par sa nouvelle valeur \(\Pr(\phi_a \vert d)\) et on exécute à nouveau le circuit de l’estimation itérative de phase.

Il nous faut encore choisir comment on met à jour la puissance \(n\) à laquelle on élève \(U\) et l’angle \(\theta\) dont on fait tourner le qubit du haut. Dans l’implémentation Q# de l’estimation Bayesienne de phase, on multiplie \(n\) par la constante \(9/8\) à chaque itération. \(\theta\) est un nombre aléatoire choisi uniformément sur un intervalle fixé.

Cette approche est optimale en termes de nombre d’application de l’opération quantique \(U\). En revanche, lorsqu’on a besoin d’une bonne précision pour l’estimation de \(\phi\), l’approche Bayésienne est très coûteuse en ressources classiques. En effet pour \(m\) bits de précision sur \(\phi\), chaque itération demande de l’ordre de \(2^m\) calculs classiques pour mettre à jour notre connaissance de \(\phi\). Dans certains cas, cette complexité exponentielle en \(m\) est trop grande. On cherche alors à réaliser des calculs plus courts, qui approximent l’inférence Bayésienne.

L’estimation robuste de phase

L’estimation robuste de phase apprend les bits de \(\phi\) un par un, en réalisant plus de mesures pour apprendre les bits de poids plus forts. C’est-à-dire que si la meilleure approximation de \(\frac{\phi}{2\pi}\) s’écrit \(\frac{\phi_1}{2} + \frac{\phi_2}{4} + ... + \frac{\phi_m}{2^m}\), c’est pour apprendre le bit \(\phi_1\) qu’on réalise le plus de mesures, puis pour le bit \(\phi_2\) et ainsi de suite jusqu’au bit \(\phi_m\).

Comme l’estimation de chaque bit \(\phi_i\) dépend de résultats de mesure, ce sont des variables aléatoires. On peut s’intéresser à la distribution de probabilité que cela définit sur la valeur \(\phi\) estimée. D’après la documentation Q#, l’écart-type de cette variable aléatoire \(\phi\) décroit comme \(\frac{c}{Q}\), où \(Q\) est le nombre d’applications de la porte \(U\) et \(c\) est une constante dont la valeur est donnée.

De façon cruciale, l’estimation robuste de phase utilise pour apprendre chaque bit \(\phi_i\) une quantité de ressources classiques (mémoire et temps de calcul) proportionnelle à \(m - i\). C’est une amélioration exponentielle en ce paramètre par rapport à l’estimation Bayésienne de phase. De plus on sait qu’aucun algorithme ne peut faire mieux que \(\frac{\tilde{c}}{Q}\) pour la décroissance de l’écart-type en fonction du nombre d’applications de \(U\). A nombre d’applications de \(U\) égal, si l’estimation robuste de phase est moins précise que l’estimation Bayésienne de phase, ça ne peut donc être que d’un facteur constant.

On peut nuancer l’avantage en temps d’exécution de l’estimation robuste par rapport à l’estimation Bayésienne en remarquant que lorsqu’on ne dispose pas de meilleur moyen d’appliquer \(U^n\) que d’appliquer \(n\) fois l’opération \(U\), le nombre \(Q\) d’appel à \(U\) est exponentiel en \(m\) dans les deux cas. Toutefois il existe des cas - comme la factorisation - où on connait des raccourcis pour appliquer \(U^n\) bien plus rapidement qu’en appliquant \(n\) fois \(U\). Dans ces cas, l’avantage en temps d’exécution de l’estimation robuste est encore plus significatif.

Les détails de l’estimation robuste de phase sont donnés dans la partie V de cet article de Kimmel, Low et Yoder. On y trouve également la justification du terme robuste : l’estimation est robuste face à des erreurs de préparation, de mesure, et d’opération quantique. L’implémentation Q# de l’estimation robuste de phase fait partie de la bibliothèque standard Q#.

L’estimation de phase par marche aléatoire

L’estimation de phase par marche aléatoire est la plus proche conceptuellement de l’estimation Bayésienne de phase. Pour que les calculs classiques entre deux itérations ne soient pas trop coûteux, on se restreint à un modèle Gaussien pour \(\phi\). Dit autrement, les distributions de probabilités envisagées pour \(\phi\) sont des lois normales, dont on met à jour à chaque itération les deux paramètres : l’espérance \(\mu\) et la variance \(\sigma^2\).

En pratique, à chaque itération on calcule l’espérance \(\mu\) et la variance \(\sigma^2\) de la distribution de probabilité a posteriori (c’est-à-dire étant donné le résultat de la mesure du qubit du haut). Puis on utilise comme distribution de probabilité a priori pour l’itération suivante, une loi normale centrée sur \(\mu\) et d’écart-type \(\sigma\). Cette approximation permet de faire beaucoup moins de calcul classique que dans le cas de l’estimation Bayésienne.

A chaque itération, on utilise pour \(\theta\) la valeur moyenne \(\mu\) obtenue à l’itération précédente et pour la puissance \(n\) à laquelle on élève \(U\) un entier proche de \(\frac{1}{\sigma}\), où \(\sigma\) est l’écart-type obtenu à l’itération précédente. Enfin, le nouveau \(\sigma\) est égal à l’ancien multiplié par la constante \(\sqrt{ \frac{e-1}{e} }\) (strictement inférieure à 1).

L’implémentation Q# de l’estimation de phase par marche aléatoire met en lumière l’emploi du terme marche aléatoire : on voit que la valeur \(\mu\), qui représente l’estimation de \(\phi\), se déplace à chaque itération d’un pas proportionnel à \(\sigma\). La direction du pas dépend du résultat de la dernière mesure.

Temps continu (t) vs temps discret (n)

Selon la façon dont on accède à la porte quantique \(U\) dont on cherche à estimer une valeur propre, on va utiliser un algorithme d’estimation de phase en temps continu ou en temps discret.

Si notre connaissance de \(U\) provient d’une description de l’Hamiltonien associé, on peut implémenter \(U(t)\) pour toute valeur positive de \(t\). En effet l’équation de Schrödinger signifie que l’Hamiltonien \(H\) est le générateur infinitésimal de l’évolution \(U(t)\). C’est-à-dire que \(U(t)\) est déterminée par \(H\) :

\[U(t) = \exp ( \frac{H}{i \hbar} t)\]

Si en revanche, on n’a pas d’autre information sur \(U\) que la possibilité de l’appliquer à un état quantique, on ne peut pas implémenter \(U^{1.5}\). On ne peut qu’implémenter \(U^n\) pour un entier naturel \(n\) : il suffit d’appliquer \(n\) fois de suite \(U\).

L’accès à \(U(t)\) (temps continu) fournit automatiquement un accès à \(U^n\) (temps discret) : il suffit d’implémenter \(U(n)\). Mais l’inverse n’est pas immédiat. En Q#, on utilise les types ContinuousOracle et DiscreteOracle pour représenter les accès à \(U\) en temps continu et en temps discret. Certaines variantes de l’estimation de phase s’expriment plus facilement en temps continu et sont donc implémentées en Q# avec un oracle continu en input.

Néanmoins, conceptuellement, ces deux cas de figures ne font pas de différence importante et c’est pourquoi nous nous sommes concentrés dans cet article sur le cas du temps discret.

Contraintes architecturales et comparaison des variantes

L’estimation quantique est la plus exigente en termes de hardware quantique : elle suppose qu’on dispose d’un grand nombre de qubits et d’un faible taux d’erreur.

L’estimation Bayésienne est la plus exigente en termes de hardware classique : elle requiert un calcul classique exponentiellement long en le nombre de bits de précision recherché à chaque itération. De plus il faut être capable de garder en mémoire quantique l’état propre \(\vert \psi \rangle\) pendant ce temps de calcul classique.

L’estimation par marche aléatoire a l’inconvénient d’être adaptative : les paramètres de la nouvelle itération dépendent des résultats de la mesure de l’itération précédente. D’une part cela rend impossible une parallélisation directe du calcul. D’autre part cela demande une communication très rapide entre le processeur quantique et la version compilée du programme à exécuter. C’est problématique pour certaines architectures d’ordinateur quantique.

A mon avis, l’estimation robuste de phase est aujourd’hui la méthode la plus prometteuse. Bien entendu, cette affirmation est à nuancer car selon le cas d’usage retenu, chaque version de l’estimation quantique a ses avantages.