Calcul quantique versus Monte Carlo

Lorsqu’on est dans la file d’attente d’une boulangerie, on ne peut pas dire de façon déterministe le moment où ce sera notre tour. Mais on peut en donner une description probabiliste : avec une certaine probabilité, ce sera notre tour dans 2 minutes, avec une autre probabilité dans 5 minutes, et ainsi de suite. Armé d’un tel modèle, on aimerait pouvoir dire dans combien de temps ce sera notre tour en moyenne. Une approche possible pour calculer cette valeur est l’approche Monte Carlo : on simule un grand nombre de fois la situation et on fait la moyenne des temps d’attente obtenus. Combien de simulations faut-il faire pour obtenir une certaine précision sur le temps d’attente moyen? Comme souvent en statistiques, l’estimation converge vers la “vraie valeur moyenne” comme \(\frac{1}{\sqrt{n}}\), où \(n\) est le nombre de simulations réalisées. C’est la loi des grands nombres (ou le théorème de la limite centrale). Les algorithmes de Monte Carlo sont fondés sur cette idée : pour calculer une valeur, on utilise des tirages aléatoires et on fait une moyenne.

Nous allons maintenant voir que l’algorithme quantique d’estimation d’amplitude permet pour ce type de situation d’avoir une estimation qui converge vers la “vraie valeur moyenne” comme \(\frac{1}{n}\), c’est-à-dire beaucoup plus vite. Est-ce la fin des algorithmes de Monte Carlo? Pas forcément…

Principes d’une option financière

Prenons l’exemple d’une option financière qu’on ne peut exercer qu’à une échéance donnée, disons dans exactement 3 mois.

Je vais commencer par expliquer le fonctionnement d’une option. Un actif financier (ça peut être par exemple une action ou une marchandise) aura un certain prix, aujourd’hui inconnu, dans 3 mois. On note \(S\) (pour sous-jacent) ce prix. En achetant aujourd’hui pour un prix \(P\) (pour prime) une option pour cet actif, je me donne la possibilité d’acheter l’actif dans 3 mois à un prix \(K\) (pour strike car la lettre \(S\) est déjà prise…). Le prix \(K\) est fixé aujourd’hui.

En pratique, dans 3 mois on sera dans l’un des deux cas suivants :

• Si \(S > K\), j’exerce mon option et je gagne \(S - K\).
• Si \(S < K\), j’ai intérêt à ne pas exercer mon option et je ne gagne donc rien.

Finalement dans tous les cas, je vais donc gagner \(\max(S-K, 0)\) dans 3 mois. Comme j’ai déjà payé \(P\) juste pour acheter l’option, lorsque je fais le bilan, j’ai gagné (ou perdu si ce nombre est négatif) \(R\) (pour return) :

\[R = \max(S-K, 0) - P\]

Ce qui m’intéresse, c’est de calculer la valeur moyenne \(R\). La difficulté, c’est que la valeur de \(S\) n’est pas encore déterminée : on ne sait pas combien vaudra l’actif dans 3 mois. En revanche les valeurs de \(K\) et de \(P\) sont fixées au moment où j’achète l’option et ne posent donc pas de difficultés supplémentaires.

Même si on ne connait pas la valeur de \(S\), il est courant d’utiliser un modèle qui nous donne la distribution de \(S\). C’est-à-dire que le modèle associe une probabilité à chacune des valeurs possibles de \(S\). A partir de la formule \(R = \max(S-K, 0) - P\), on peut en déduire la distribution de \(R\). A partir de là, on peut calculer l’espérance (c’est-à-dire la valeur moyenne) de \(R\). Si l’espérance de \(R\) est positive, en moyenne et d’après mon modèle, je gagne de l’argent en achetant l’option. Au contraire si l’espérance de \(R\) est négative, je perds de l’argent en moyenne. Ma décision d’acheter ou non cette option dépend aussi du risque contre lequel je cherche à me protéger. J’espère néanmoins vous avoir convaincu qu’il est intéressant de savoir estimer l’espérance de \(R\).

Estimation Monte Carlo à l’aide d’un ordinateur classique

On suppose maintenant qu’on dispose d’une procédure \(M\) (pour marché) qui réalise le calcul suivant : on lui donne en entrée r bits aléatoires (fournis par un générateur de nombres pseudo-aléatoires) et cette procédure renvoie une valeur pour \(S\) avec une probabilité qui correspond à la façon dont on a modélisé le marché. Cette procédure \(M\) est implémentée par un ordinateur classique (i.e. non quantique). En répétant le calcul \(M\) un grand nombre de fois, en utilisant la formule ci-dessus pour calculer à chaque fois \(R\) à partir de \(S\) et en faisant la moyenne des résultats obtenus, on obtient un estimateur de l’espérance de \(R\).

On ne se pose pas ici la question de savoir comment implémenter \(M\) car cela dépend de la modélisation du marché utilisée. Mais on se demande combien de fois il faut utiliser \(M\). Comme la plupart des méthodes Monte Carlo (i.e. utilisant des tirages aléatoires), l’estimateur de l’espérance de \(R\) converge vers sa “vraie valeur” (ou du moins vers l’espérance pour la modélisation utilisée) comme \(\frac{1}{\sqrt{n}}\). \(n\) est le nombre de fois qu’on a fait appel à \(M\).

Or l’algorithme quantique d’estimation de phase permet d’estimer un paramètre avec une précision proportionnelle à \(\frac{1}{n}\), ce qui représente une amélioration quadratique ! Dans notre cas, on va avoir besoin d’une variante de l’estimation de phase : l’algorithme quantique d’estimation d’amplitude. On va aussi avoir besoin d’une opération quantique qui calcule l’espérance de \(R\) sous la forme d’une amplitude quantique. Voyons tout de suite ce que ça veut dire.

Estimation à l’aide d’un ordinateur quantique

On a besoin de deux opérations quantiques. La première modélise le marché : elle produit un état quantique correspondant à la distribution de probabilité de l’actif sous-jacent \(S\). La deuxième implémente la fonction de \(S\) dont on souhaite calculer l’espérance. Ici il s’agit de \(R\) : la variable qui représente le gain (qui peut être négatif) réalisé lorsqu’on achète une option.

Modélisation quantique de l’actif sous-jacent

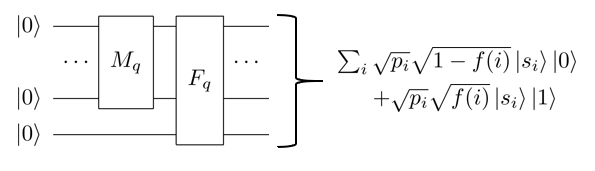
\(M_q\) est l’équivalent quantique de \(M\). Cette opération quantique prépare un état quantique correspondant à la distribution de probabilité de \(S\) :

\[M_q (\vert 0 .. 0 \rangle ) = \sum_i \sqrt{p_i} \vert s_i \rangle\]

Selon le modèle qu’on utilise ici, \(S\) prend la valeur \(s_i\) avec probabilité \(p_i\). \(M_q\) produit le “bon” état quantique pour cette situation. En effet, d’après la règle de la mesure quantique, si on mesurait l’état quantique produit par \(M_q\), on obtiendrait \(s_i\) avec probabilité \(p_i\).

Implémentation quantique de la fonction qui nous intéresse (ici \(R\))

\(F_q\) calcule \(R\) à partir de \(S\) selon la formule \(R = f(S) = \max (S-K, 0) - P\). On peut supposer qu’on accède à cette opération quantique sous la forme suivante :

\[F_q (\vert s_i \rangle \vert 0 \rangle) = \vert s_i \rangle ( \sqrt{1 - f(s_i)} \vert 0 \rangle + \sqrt{f(s_i)} \vert 1 \rangle )\]

Composition des deux opérations quantiques

Pour produire l’amplitude qu’on cherche à estimer, il ne reste plus qu’à appliquer successivement \(M_q\) et \(F_q\). Comme \(F_q\) prend en entrée un qubit de plus que \(M_q\), on utilise l’opération \(M_q \otimes I\) pour signifier que \(M_q\) n’agit pas sur ce qubit supplémentaire :

\[F_q (M_q \otimes I) (\vert 0 .. 0 \rangle \otimes \vert 0 \rangle) = \sum_i \sqrt{p_i} \sqrt{1 - f(s_i)} \vert s_i \rangle \vert 0 \rangle + \sqrt{p_i} \sqrt{f(s_i)} \vert s_i \rangle \vert 1 \rangle\]

C’est plus clair sous la forme d’un circuit quantique :

L’amplitude associée à chaque état \(\vert s_i \rangle \vert 1 \rangle\) vaut \(\sqrt{p_i f(s_i)}\). Ce qui nous intéresse ici, c’est l’amplitude associée à tout l’espace vectoriel (qu’on notera \(E\)) où le qubit de droite est dans l’état \(\vert 1 \rangle\). Il faut donc ajouter les carrés de toutes ces amplitudes pour obtenir le carré de l’amplitude \(A_E\) :

\[A_E^2 = \sum_i p_i f(s_i)\]

En appliquant l’algorithme quantique d’estimation d’amplitude, on peut estimer \(A_E^2\). C’est exactement la quantité qui nous intéresse : l’espérance de \(R\). On obtient ainsi une estimation de l’argent qu’on va gagner (ou perdre) en moyenne en achetant l’option.

A propos de l’algorithme quantique d’estimation d’amplitude

L’estimation d’amplitude est un très bel algorithme quantique qui peut être considéré comme le produit de deux autres algorithmes quantiques :

• l’amplification d’amplitude (une généralisation de l’algorithme quantique de Grover).
• l’estimation de phase.

Cet article décrit en détail l’amplification et l’estimation d’amplitude. Comme l’estimation de phase (et pour les mêmes raisons), l’estimation d’amplitude fournit une accélération quadratique par rapport à une estimation classique de paramètre : l’estimateur converge vers la “vraie valeur” comme \(\frac{1}{n}\) alors qu’un estimateur classique converge comme \(\frac{1}{\sqrt{n}}\). \(n\) correspond au nombre de répétitions et est donc proportionnel au temps de calcul.

L’estimation d’amplitude requiert trois opérations quantiques :

• L’opération quantique qui produit l’amplitude. Ici il s’agit de l’application successive de \(M_q\) et de \(F_q\).
• L’opération quantique qui marque le sous-espace d’arrivée : celui sur lequel est produit l’amplitude qui nous intéresse. Ici il s’agit de l’espace pour lequel le qubit de droite est dans l’état \(\vert 1 \rangle\). Une simple porte quantique \(Z\) appliquée à ce qubit de droite fait donc l’affaire.
• L’opération quantique qui marque l’état de départ. Ici (comme souvent), il s’agit de l’état \(\vert 0 .. 0 \rangle\). Cette opération quantique ne dépend pas du problème considéré et on sait l’implémenter de façon efficace. On peut donc ne plus y penser.

Il est aussi nécessaire de pouvoir implémenter l’inverse de l’opération qui produit l’amplitude qui nous intéresse. Si cette opération est implémentée sous la forme d’un circuit quantique (c’est généralement le cas), il suffit d’implémenter l’inverse de chaque porte quantique dans l’ordre inverse. Ce n’est donc pas plus difficile d’implémenter l’inverse d’une opération que d’implémenter l’opération elle-même. De plus certains langages de programmation quantique comme Q# génèrent automatiquement l’inverse (on dit aussi l’adjoint) d’une opération quantique.

Limites de l’approche quantique

• Contrairement au Monte Carlo classique, il n’est pas possible de paralléliser ce calcul quantique. Comme tous les algorithmes quantiques d’amplification ou d’estimation de phase ou d’amplitude, les opérations quantiques doivent être appliquées de façon séquentielle.

• On s’est intéressé ici à la façon dont la précision de l’estimation dépend du nombre d’appels aux opérations quantiques \(M_q\) et \(F_q\). Cela ne nous dit pas comment construire ces opérations quantiques. Comme cela dépend de la façon dont on modélise un marché et de la variable dont l’espérance nous intéresse, il est difficile de donner des résultats généraux à ce sujet. En pratique pour chaque calcul Monte Carlo, il faut trouver une façon efficace de réaliser ces deux opérations quantiques. Selon la façon dont on implémente ces deux opérations, la précision à partir de laquelle l’algorithme quantique est plus rapide que l’algorithme classique sera plus ou moins grande.

Conclusion

Le remplacement d’un calcul Monte Carlo classique par l’approche quantique d’estimation d’amplitude est toujours possible. On retrouvera toujours l’accélération quantique quadratique pour la vitesse de convergence de l’estimation. Néanmoins il faut aussi tenir compte du temps de calcul associé au calcul de la grandeur qui nous intéresse sous la forme d’une amplitude quantique. Selon la précision recherchée et la facilité à implémenter l’équivalent des opérations \(M_q\) et \(F_q\) pour un cas d’usage donné, l’approche quantique présentera ou non un temps de calcul plus court que l’approche Monte Carlo classique.

J’ai choisi ici d’illustrer l’algorithme quantique d’estimation d’amplitude à l’aide d’un cas d’usage issu de la finance. Néanmoins tout utilisateur d’une méthode de Monte Carlo peut se poser la question d’utiliser plutôt une approche quantique.