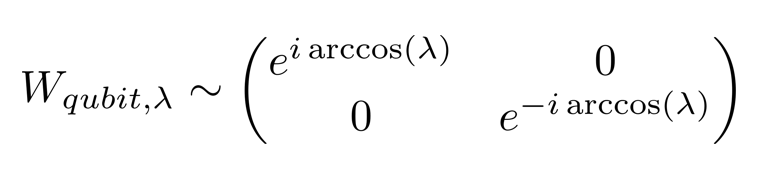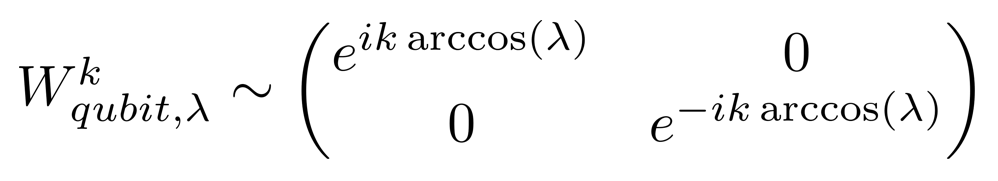Qubitisation

La qubitisation est une méthode qui a été proposée en 2016 dans le cadre de la simulation Hamiltonienne. La simulation Hamiltonienne est essentielle en chimie quantique pour favoriser une réaction de capture du carbone par exemple ou pour trouver d’autres réactions chimiques. La simulation Hamiltonienne permet également d’étudier de nombreux modèles de physique quantique avec des applications en physique des matériaux (matériaux plus résistants, plus isolants, supraconducteurs à température ambiante, …). Dans certains cas, la qubitisation remplace avantageusement des techniques de simulation Hamiltonienne plus ancienne comme la Trotterisation. De façon plus générale, elle fournit un cadre conceptuel nouveau et très utile pour la compréhension et la découverte d’algorithmes quantiques. L’intérêt de la qubitisation dépasse aujourd’hui le cadre de la simulation Hamiltonienne et s’applique par exemple au domaine des marches quantiques.

La qubitisation consiste à réaliser un calcul dans un espace vectoriel de dimension au moins deux fois plus grande que la dimension de l’espace vectoriel qui nous intéresse vraiment. En calcul quantique, le plongement dans un espace de dimension double ne coûte pas très cher : un seul qubit auxiliaire suffit à doubler la dimension de l’espace vectoriel permettant de représenter l’information quantique en cours de traitement. En effet on utilise un espace vectoriel de dimension \(2^n\) pour représenter l’état quantique de \(n\) qubits.

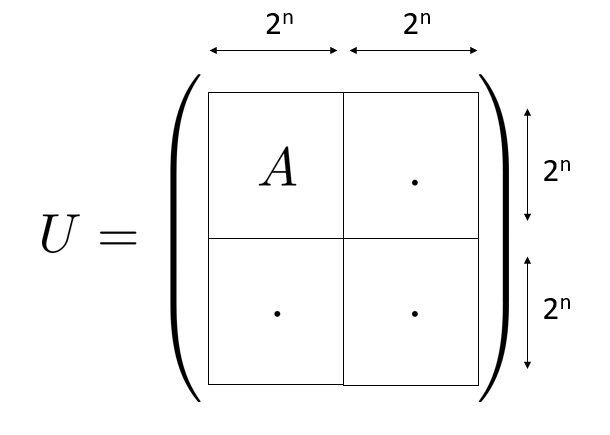
De façon plus générale, la qubitisation s’appuie sur la technique d’encodage par blocs : on suppose qu’on sait réaliser un circuit quantique tel que la matrice unitaire \(U\) représentant ce circuit encode l’opérateur qui nous intéresse, qu’on notera désormais sous la forme d’une matrice \(A\). Pour fixer les idées, on peut imaginer que \(A\) est une matrice de taille \(2^n \times 2^n\) et que \(U\) est une matrice unitaire de taille \(2^{n+1} \times 2^{n+1}\). Toujours pour fixer les idées, on va se concentrer dans ce billet de blog sur le cas où \(A\) est diagonalisable et possède \(2^n\) valeurs propres distinctes.

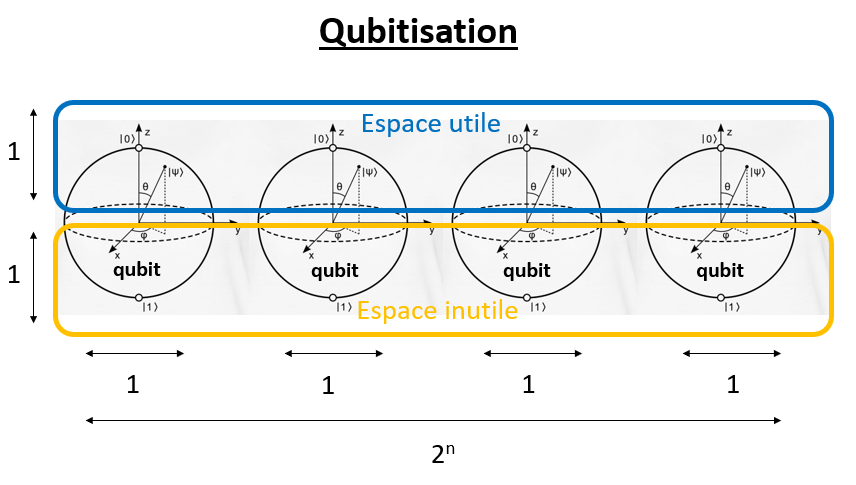
Conceptuellement, la qubitisation repose sur une décomposition de l’espace de dimension \(2^{n+1}\) sur lequel agit \(U\) en \(2^n\) espaces de dimension \(2\) de façon à ce que chaque espace de dimension \(2\) soit engendré par un vecteur propre de \(A\) et un vecteur “inutile”, c’est-à-dire sur lequel \(A\) n’agit pas. Le terme qubitisation fait référence à cette décomposition en espaces de dimension 2 : chaque espace propre de \(A\) est plongé dans un espace de dimension \(2\), c’est-à-dire l’espace d’un qubit.

On peut donc penser à \(\tilde U\), l’opération quantique obtenue en qubitisant \(U\), comme à la somme directe de \(2^n\) matrices unitaires de dimension \(2\). On a une unitaire de dimension \(2\) par valeur propre de \(A\):

\[\tilde U = \oplus_{\lambda \in Sp(A)} W_{qubit, \lambda}\]

\(W_{qubit, \lambda}\) est une matrice de taille \(2 \times 2\). En tant que matrice unitaire, elle est diagonalisable et ses valeurs propres ont pour module \(1\). De plus ses valeurs propres sont déterminées par \(\lambda\) : ce sont \(e^{i \arccos(\lambda)}\) et \(e^{-i \arccos(\lambda)}\).

La qubitisation permet ainsi de réaliser un tour de force ! Chaque valeur propre est isolée dans un espace de dimension 2 à l’intérieur duquel on va pouvoir la processer sans que ce signal ne vienne se mélanger aux signaux des autres valeurs propres. On peut dorénavant appliquer un même traitement à toutes les valeurs propres en parallèle puisque le signal correspondant à chaque valeur propre va rester à l’intérieur de l’espace de dimension 2 qui lui est réservé.

De façon cruciale, on peut appliquer de façon séquentielle l’encodage par bloc de la matrice \(A\). Si on s’y prend bien, chaque espace qubitisé évolue individuellement sans interférer avec les autres espaces qubitisés. Si on n’applique pas d’autres portes quantiques que le strict nécessaire, l’application de \(k\) encodages par bloc de la matrice \(A\) fournit l’encodage par bloc d’une matrice \(A_{(k)}\) entièrement caractérisé par \(A\) :

1. \(A_{(k)}\) a les mêmes espaces propres que \(A\).
2. Pour chaque espace propre, la valeur propre de \(A_{(k)}\) est obtenue à partir de celle de \(A\) en appliquant le \(k^{ième}\) polynôme de Tchebychev : \(\lambda_{(k)} = \cos(k \arccos(\lambda))\).

 

On comprend facilement que les valeurs propres de \(A_{(k)}\) soient celles de \(A\) auxquelles on a appliqué le \(k^{ième}\) polynôme de Tchebychev en regardant la puissance \(k^{ième}\) de \(W_{qubit, \lambda}\) :

On peut aller encore plus loin que la qubitisation en utilisant les techniques de traitement quantique du signal. Il se trouve d’ailleurs que ces deux avancées majeures en algorithmique quantique ont été introduites dans le même article : Hamiltonian Simulation by Qubitization. Le traitement quantique du signal est fondé sur la théorie de l’approximation de fonctions par des polynômes de Tchebychev. Etant donné une fonction \(f\), Il est donc possible d’approximer l’encodage par bloc d’une matrice \(A_f\) qui garde la structure d’espaces propres de \(A\) mais modifie son spectre selon la fonction \(f\) :

1. \(A_{f}\) a les mêmes espaces propres que \(A\).
2. Pour chaque espace propre, la valeur propre de \(A_{f}\) est obtenue à partir de celle de \(A\) en appliquant la fonction \(f\) : \(\lambda_{f} = f(\lambda)\).

 

Application à la simulation Hamiltonienne

La simulation Hamiltonienne est la motivation des auteurs de l’article sur la qubitisation. Etant donné une description d’un Hamiltonien \(H\), Le but de la simulation Hamiltonienne est d’approximer l’évolution \(U(t)\) donnée par l’équation de Schrödinger :

\[U_{Schroedinger}(t) = e^{-i \frac{H t}{\bar{h}}}\]

Il se trouve que par qubitisation, il est plus facile d’implémenter l’opération quantique suivante :

\[U_{qubitisation}(t) = e^{-i \frac{\arccos(\frac{H}{\alpha}) t}{\bar{h}}}\]

où \(\alpha\) est une constante de normalisation telle que toutes les valeurs propres de \(\frac{H}{\alpha}\) soit comprise entre \(-1\) et \(1\). Il est courant que le but de la simulation Hamiltonienne soit de calculer différents niveaux d’énergie associés à un Hamiltonien. Dans ce cas il est suffisant d’implémenter \(U_{qubitisation}\). En effet, après avoir estimé une valeur propre de \(U_{qubitisation}\), on en déduit la valeur de l’énergie correspondante en prenant simplement le cosinus de la bonne quantité. Si jamais on a absolument besoin d’implémenter l’opération quantique \(U_{Schroedinger}\), c’est également possible pour un faible surcoût grâce aux techniques du traitement quantique du signal.

Application à d’autres domaines en algorithmique quantique

En 2018, l’article Quantum singular value transformation and beyond: exponential improvements for quantum matrix arithmetics reprend les techniques de qubitisation et les généralise. Cet article est important conceptuellement parce qu’il réexplique un certain nombre de résultats connus en algorithmique quantique à travers le prisme du traitement quantique du signal (ou de sa généralisation la transformation quantique de valeurs singulières). On retrouve les algorithmes quantiques suivants :

1. Implémentation de l’inverse d’une matrice.
2. Amplification d’amplitude à point fixe.
3. Amplification d’amplitude robuste et ignorante (oblivious).
4. Certaines marches quantiques.

Pour une liste plus exhaustive je vous conseille la lecture de l’article ci-dessus sur la transformation quantique de valeurs singulières.

Conclusion

La qubitisation permet de transformer un opérateur \(A\) dont le spectre est inclus dans \([-1, 1]\) en un opérateur unitaire \(U\) ayant une structure d’espaces propres similaire et une valeur propre \(\theta = \arccos(\lambda)\) pour chaque valeur propre \(\lambda\) de \(A\). Il est courant de commencer par normaliser \(A\) de façon à ce que son spectre soit inclus dans \([-1, 1]\) avant de le qubitiser. Il est ensuite possible d’appliquer une même fonction à chaque valeur propre. Pour implémenter l’inverse d’une matrice par exemple, on peut appliquer la fonction \(x \mapsto \frac{1}{x}\) à chaque valeur propre \(\lambda\).

Le fait d’appliquer la fonction \(\arccos\) aux valeurs propres est particulièrement intéressant lorsqu’une valeur propre a sa valeur absolue \(\vert \lambda \vert\) proche de \(1\). En effet, pour \(\theta\) proche de \(0\),

\[\cos(\theta) \approx 1 - \frac{\theta^2}{2}.\]

Dit autrement, pour \(\lambda\) proche de \(1\),

\[\arccos(\lambda) \approx \sqrt{2} \sqrt{1 - \lambda}.\]

La transformation par la fonction \(\arccos\) donne ainsi un nouvel éclairage sur les accélérations quadratiques des algorithmes d’amplification d’amplitude et de certaines marches quantiques. En effet dans le cas des marches quantiques par exemple, le facteur \(\sqrt{1 - \lambda}\) montre que le trou spectral augmente de façon quadratique lorsqu’on applique la fonction \(\arccos\).

La qubitisation fournit ainsi un cadre très général qui permet d’expliquer les accélérations de nombreux algorithmes quantiques.