Quantum Computing | Calcul quantique : la technique du retour de phase

Le retour de phase (en anglais “phase kickback”) est le point fondamental des algorithmes quantiques d’estimation de phase. Or l’estimation de phase est la sous-routine centrale de la simulation moléculaire quantique, de l’algorithme quantique de factorisation (c’est-à-dire de l’algorithme de Shor) et de l’algèbre linéaire quantique. A son tour, la simulation moléculaire ouvre la porte à la découverte de nouveaux matériaux, de nouvelles réactions chimiques et de nouveaux médicaments. De même l’algèbre linéaire quantique est à l’origine de nombreuses applications du calcul quantique : l’optimisation convexe et toutes ses applications, une partie importante du machine learning quantique et la résolution d’équations aux dérivées partielles.

Par ailleurs, une façon un peu différente de comprendre le retour de phase est utilisée pour adapter une fonction classique en une opération quantique qui peut acquérir de l’information en parallèle sur tous les inputs possibles de la fonction classique. Cette adaptation d’une fonction classique en une opération quantique est fondamentale pour les algorithmes quantiques de Deutsch-Josza et d’amplification d’amplitude (c’est-à-dire Grover et ses généralisations) par exemple.

On peut donc sans éxagérer dire que la quasi-totalité des algorithmes quantiques utilisent sous une forme ou sous une autre la technique du retour de phase. Je vais maintenant donner une explication détaillée de cette brique fondamentale de l’algorithmique quantique.

Retour de phase et algorithmes d’estimation de phase

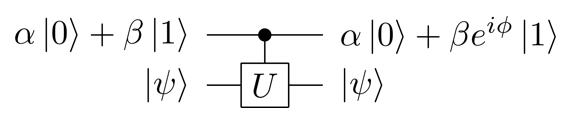
Le retour de phase correspond au circuit suivant:

On suppose ici que l’état $\vert \psi \rangle$ est un état propre de la porte $U$. C’est à dire que lorsqu’on applique $U$ à l’état $\vert \psi \rangle$, il acquiert une phase $\phi$:

$$ U \vert \psi \rangle = e^{i\phi} \vert \psi \rangle. $$

L’état $\vert \psi \rangle$ peut être constitué d’un ou de plusieurs qubits. En revanche dans cet exemple, la ligne du haut correspond à un seul qubit, qu’on va appeler le qubit de contrôle. Le qubit de contrôle peut être dans un état de superposition quelconque. En suivant la convention standard, je note ici $\alpha \vert 0 \rangle + \beta \vert 1 \rangle$ cet état de superposition quelconque.

La matrice $U$ est contrôlée par le qubit de contrôle. C’est-à-dire qu’elle est appliquée uniquement lorsque le qubit de contrôle est dans l’état $\vert 1 \rangle$, seule cette partie de la superposition acquiert la phase $\phi$. Comme la phase est une propriété de l’ensemble des qubits, on peut considérer que l’état $\vert \psi \rangle$ n’acquiert jamais la phase $\phi$ mais que la partie $\vert 1 \rangle$ du qubit de contrôle l’acquiert.

Finalement l’état $\vert \psi \rangle$ n’est pas modifié. Il peut donc être réutilisé. En revanche le qubit de contrôle a enregistré de l’information sur $\phi$, c’est-à-dire sur une propriété de l’état $\vert \psi \rangle$ et de la matrice $U$.

Ce point de vue est très contre-intuitif car on pourrait dire naïvement que l’état du qubit de contrôle n’est pas modifié et que l’état $\vert \psi \rangle$ est modifié lorsque le qubit de contrôle est dans l’état $\vert 1 \rangle$. Mais ce même point de vue est très instructif car il montre que la ressource précieuse (l’état $\vert \psi \rangle$) n’est pas modifiée par cette opération quantique.

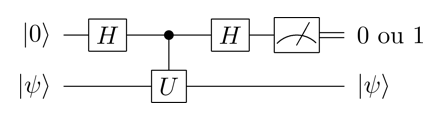
Après un éventuel post-traitement, on peut mesurer le qubit de contrôle pour obtenir de l’information sur $\phi$. Un circuit très simple qui permet de récupérer de l’information sur $\phi$ est le suivant:

La porte $H$ est la porte de Hadamard et le symbole représentant une jauge signifie qu’on mesure le qubit correspondant à la ligne sur laquelle est placé ce symbole.
Lorsqu’on réalise ce circuit quantique, le résultat de la mesure du qubit de contrôle est $0$ avec probabilité $\cos^2(\frac{\phi}{2})$ et $1$ avec probabilité $\sin^2(\frac{\phi}{2})$. Chaque exécution de ce circuit quantique apporte donc un peu d’information sur $\phi$.

Toutes les variantes de l’estimation de phase sont fondées sur le retour de phase. Selon le nombre de qubits de contrôle, selon les itérées de $U$ qui sont appliquées ($U^2$, $U^3$, $U^4$, …), selon le post-traitement du ou des qubits de contrôle et selon que ce ou ces qubits de contrôles soient immédiatement mesurés ou non, l’algorithme s’appellera estimation quantique de phase standard ou estimation quantique de phase de Kitaev ou encore une des différentes variantes d’estimation itérative de phase :

l’estimation bayésienne de phase.
l’estimation robuste de phase.
l’estimation de phase par marche aléatoire.

Retour de phase et “quantification” d’un calcul classique

La technique du retour de phase n’est pas seulement utile pour l’estimation de phase. Le retour de phase permet également d’exprimer un calcul classique sous la forme d’une opération quantique qui enregistre pour chaque input possible le résultat du calcul dans la phase de l’état quantique correspondant à cet input. C’est à cette possibilité qu’il est parfois fait allusion par l’expression un peu floue de “parallélisme quantique”.

Oracle à qubit auxiliaire

Considèrons une fonction booléenne, c’est-à-dire une fonction qui prend $n$ bits en entrée et en renvoie un seul en sortie $f : \{0, 1\}^n \rightarrow \{0, 1\}$. Ce cadre peut paraitre restrictif à première vue mais il permet en fait d’exprimer n’importe quel calcul classique (un calcul classique qui renvoie $m$ bits en sortie peut être décrit par $m$ fonctions $f_1, \, \dots, f_m$).

Pour ne pas perdre d’information pendant un calcul quantique, on implémente généralement ce type d’opération en laissant les $n$ qubits d’input inchangés et en utilisant un qubit supplémentaire (dit qubit auxiliaire) pour enregistrer le résultat de la fonction. $U_f$ est l’opération quantique qui correspond à la fonction $f$:

$$ U_f ( \, \vert x \rangle \vert 0 \rangle \, ) = \vert x \rangle \vert f(x) \rangle. $$

On voit que les qubits d’inputs sont dans l’état $\vert x \rangle$ avant et après l’application de l’opération quantique $U_f$. En revanche le qubit auxiliaire passe de l’état $\vert 0 \rangle$ à l’état $\vert f(x) \rangle$. C’est-à-dire ou bien $\vert 0 \rangle$ ou bien $\vert 1 \rangle$ selon la valeur de $f(x)$.
Si le qubit auxiliaire était dans l’état $\vert 1 \rangle$ avant l’application de $U_f$, il se retrouverait dans l’état $\vert \text{NOT}(f(x)) \rangle$ après l’application de $U_f$. En effet on ajoute la valeur de $f(x)$ à la valeur initiale du qubit auxiliaire. Comme $1 + 1 = 0$ en binaire, on retrouve bien le résultat annoncé. Pour rappel :

$$ \text{NOT}(0) = 1 \quad \text{ et } \quad \text{NOT}(1) = 0. $$

Oracle à phase

Souvent en algorithmique quantique, on préfère enregistrer le résultat de la fonction $f$ sans utiliser de qubit auxiliaire. On peut atteindre ce but en enregistrant ce résultat directement dans la phase de chaque état quantique:

$$ \tilde{U}_f ( \, \vert x \rangle \, ) = ({\color{red} -}1)^{f(x)} \vert x \rangle. $$

Dit autrement, si $f(x) = 0$, alors $\tilde{U}_f ( \, \vert x \rangle \, ) = \vert x \rangle$. L’état $\vert x \rangle$ reste inchangé.

Et si $f(x) = 1$, alors $\tilde{U}_f ( \, \vert x \rangle \, ) = {\color{red} -} \vert x \rangle$. L’état $\vert x \rangle$ acquière la phase ${\color{red} -}1$.

Il est souvent plus facile d’implémenter l’opération quantique $U_f$ (sans $\tilde{}$), qu’on appellera désormais l’oracle à qubit auxiliaire. En effet on peut adapter le circuit classique qui permet de calculer $f$ pour obtenir le circuit quantique qui permet de calculer $U_f$.
En revanche dans de nombreux algorithmes quantiques comme par exemple l’algorithme de Grover ou l’algorithme de Deutsch-Jozsa, on a besoin de l’opération quantique $\tilde{U}_f$ (avec $\tilde{}$), qu’on appellera désormais l’oracle à phase. En plus l’oracle à phase est plus concis et il est plus facile de se le représenter à mon avis. Il permet de bien comprendre ce qu’est (et ce que n’est pas) le parallélisme quantique : en une seule opération quantique, chaque état quantique $\vert x \rangle$ associé à chacun des $2^n$ inputs possible $x$ encode son résultat $f(x)$ dans sa phase.

Heureusement la technique du retour de phase permet de transformer un oracle à qubit auxiliaire (plus naturel à implémenter) en un oracle à phase (plus utile en algorithmique quantique).

D’un oracle à l’autre

Pour obtenir un oracle à phase:

On applique une porte $X$ puis une porte de Hadamard au qubit auxiliaire.
On applique l’oracle à qubit auxiliaire au système constitué des qubits d’input et du qubit auxiliaire.
On applique une porte de Hadamard puis une porte $X$ au qubit auxiliaire.

Vérifions qu’on obtient bien la transformation attendue (c’est-à-dire $\tilde{U}_f$) pour chaque état $\vert x \rangle$ des qubits d’input.

Les portes $X$ et de Hadamard permettent de mettre le qubit auxiliaire dans l’état $\frac{1}{\sqrt{2}} ( \vert 0 \rangle - \vert 1 \rangle)$.

1er cas : f(x)=0

L’oracle à qubit auxiliaire n’a aucun effet dans ce cas.

La porte de Hadamard et la porte $X$ remettent le qubit auxiliaire dans l’état $\vert 0 \rangle$.

Les qubits d’inputs sont restés dans l’état $\vert x \rangle$.

2eme cas : f(x)=1

L’oracle à qubit auxiliaire change la partie $\vert 0 \rangle$ du qubit auxiliaire en $\vert 1 \rangle$ et sa partie $\vert 1 \rangle$ en $\vert 0 \rangle$. Ainsi après application de l’oracle à qubit auxiliaire, le qubit auxiliaire est dans l’état:

$$ \frac{1}{\sqrt{2}} ( \vert 1 \rangle - \vert 0 \rangle) = {\color{red} -} \frac{1}{\sqrt{2}} ( \vert 0 \rangle - \vert 1 \rangle) $$

Comme la phase est une propriété globale du système, on peut considérer que le qubit auxiliaire est dans l’état $\frac{1}{\sqrt{2}} ( \vert 0 \rangle - \vert 1 \rangle)$ et que les qubits d’input sont dans l’état ${\color{red} -} \vert x \rangle$.

La porte de Hadamard et la porte $X$ remmettent finalement le qubit auxiliaire dans l’état $\vert 0 \rangle$.

Bilan

On voit que dans les deux cas, le qubit auxiliaire revient à son état de départ (c’est-à-dire $\vert 0 \rangle$) et l’état des qubits d’input passe de $\vert x \rangle$ à $({\color{red} -} 1)^{f(x)} \vert x \rangle$. On a donc réussi à construire un oracle à phase à partir d’un oracle à qubit auxiliaire.

Il semble plus facile d'obtenir un oracle à phase à partir d'un oracle à qubit auxiliaire que d'obtenir l'oracle de Matrix à partir de l'oracle de Delphes.

Explication en termes de retour de phase

Le calcul qu’on a fait dans la partie précédente montre que l’état $\frac{1}{\sqrt{2}} ( \vert 0 \rangle - \vert 1 \rangle)$, qu’on notera désormais $\vert - \rangle$, est un état propre de la porte $X$ avec valeur propre ${\color{red} -} 1$:

$$ X \vert - \rangle = {\color{red} -} \vert - \rangle. $$

En effet $X \vert 0 \rangle = \vert 1 \rangle$ et $X \vert 1 \rangle = \vert 0 \rangle$.

De plus appliquer un oracle à qubit auxiliaire revient à appliquer une porte $X$ au qubit auxiliaire en contrôlant sur les états $\vert x \rangle$ tels que $f(x)=1$ (c’est-à-dire qu’on applique la porte $X$ uniquement lorsque $f(x) = 1$). Attention à ne pas confondre la porte $X$ qui est l’analogue quantique d’une porte NOT et la variable $x$ qui représente l’un des $2^n$ inputs possibles.

Par retour de phase, seuls les états $\vert x \rangle$ tels que $f(x)=1$ vont acquérir la valeur propre de l’état $\vert - \rangle$ pour la porte $X$, c’est-à-dire la phase ${\color{red} -} 1$.

Conclusion

La transformation d’un oracle à qubit auxiliaire en un oracle à phase fournit un deuxième cas d’utilisation de la technique du retour de phase. Dans ce cas les qubits d’input acquièrent de l’information et le qubit auxiliaire joue le rôle de l’état propre $\vert \psi \rangle$.
A l’inverse dans le cas de l’estimation de phase, le qubit auxiliaire acquière de l’information et l’état propre $\vert \psi \rangle$ est laissé inchangé.

On retrouve au moins l’une de ces utilisations dans la quasi-totalité des algorithmes quantiques.