Trotterisation

La simulation Hamiltonnienne est une branche majeure de l’informatique quantique. Elle permet de décrire l’évolution dans le temps d’un système physique. De plus connaître cette évolution dans le temps permet de calculer des propriétés essentielles d’un système physique, comme par exemple l’énergie de son état fondamental. On trouve de nombreuses applications de la simulation Hamiltonienne en chimie quantique, en sciences des matériaux et même en algèbre linéaire quantique.

L’analogue classique de la simulation Hamiltonienne consiste à décrire l’évolution dans le temps d’un système physique lorsqu’on connaît toutes les forces extérieures qui s’appliquent à ce système. Depuis Newton, on utilise alors généralement le principe fondamental de la dynamique : la somme des forces est égale à la masse multipliée par l’accélération. Si on connaît également les position et vitesse initiales du système, on peut calculer son état à tout instant ultérieur en résolvant l’équation différentielle donnée par le principe fondamental de la dynamique.

La simulation Hamiltonienne consiste à suivre la même démarche pour un système quantique. L’ensemble des forces qui s’appliquent au système est décrit sous la forme d’un Hamiltonien. Le principe fondamental de la dynamique est remplacé par l’équation de Schrödinger :

\[i \hbar \, \vert \psi'(t) \rangle = \hat{H} \vert \psi(t) \rangle.\]

Et les positions et vitesses initiales du système sont remplacées par sa fonction d’onde initiale (c’est-à-dire son état quantique initial) : \(\vert \psi (t=0) \rangle\).

Simplification du problème

Normallement \(\vert \psi(t) \rangle\) est un vecteur complexe et \(\hat{H}\) est un opérateur complexe mais … peu importe. Nous allons simplifier les choses 🧙🏻‍♂️. Si je remplace formellement \(\frac{\hat{H}}{i \hbar}\) par \(\alpha\) et \(\vert \psi \rangle\) par une fonction \(f\), j’obtiens l’équation différentielle à une seule variable réelle suivante:

\[f' = \alpha f.\]

Faire ce remplacement formel n’est pas “licite” mais c’est instructif : on peut considérer pour l’instant que c’est une analogie. Cette nouvelle équation différentielle est suffisamment simple pour qu’on en connaisse une solution analytique:

\[f(t) = f(0) e^{\alpha t}.\]

Si on connaît la valeur de f à l’instant \(t = 0\) on peut calculer sa valeur à tout autre instant.

Admettons toutefois qu’on ne connaisse pas cette solution analytique. Ou bien (comme c’est le cas pour l’équation de Schrödinger) que calculer \(e^{\alpha t}\) ne soit pas possible en pratique. Dans ce cas, on peut utiliser un schéma d’intégration numérique 👨🏻‍🔧. On définit un pas de temps \(\delta t\) suffisamment court et on utilise la formule approchée suivante :

\[f(t + \delta t) \approx f(t) + \delta t \, f'(t) = f(t) + \delta t \, \alpha \, f(t).\]

Lorsqu’on fait cette approximation pour l’équation de Schrödinger, on dit que cette solution approchée est obtenue par Trotterisation. On peut également donnée une forme multiplicative de cette approximation :

\[f(t + \delta t) \approx (1 + \delta t \, \alpha ) \times f(t).\]

En mettant bout à bout toutes ces approximations, on obtient une expression de \(f(t)\) directement en fonction de \(f(0)\) :

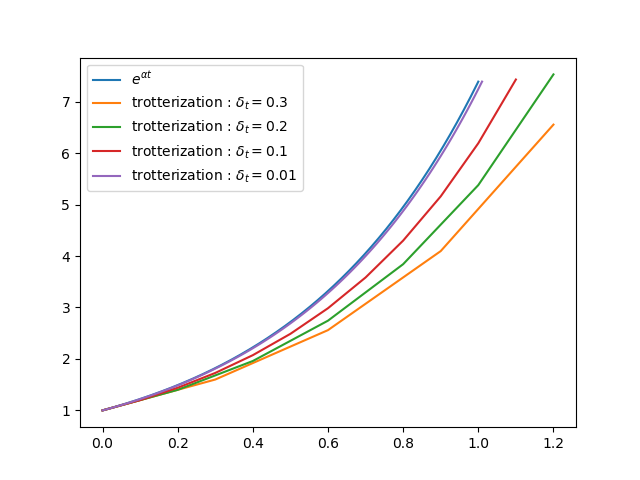
\[f(t) \approx \prod_{k = 1}^{\lfloor \frac{t}{\delta t} \rfloor} (1 + \delta t \, \alpha ) \, \, f(0).\]

Sur la courbe suivante, j’ai tracé pour \(\alpha = 2\) la vraie solution (\(e^{\alpha t}\)) et les Trotterisations associées pour différents pas de temps \(\delta t\).

Cas d’un Hamiltonien quelconque

Revenons maintenant au système quantique \(\vert \psi \rangle\) dont l’évolution est régie par l’équation de Schrödinger. En simulation Hamiltonienne, on connaît l’Hamiltonien \(\hat{H}\) qui apparait dans l’équation de Schrödinger. La solution exacte est formellement la même que dans le cas de la fonction \(f\) :

\[\vert \psi (t) \rangle = e^{\frac{\hat{H}}{i\hbar} t} \, \, \vert \psi (0) \rangle\]

La difficulté ici est que pour un système de \(n\) qubits, \(\vert \psi \rangle\) est un vecteur de dimension \(2^n\) et \(e^{\frac{\hat{H}}{i\hbar}}\) est une matrice carrée de taille \(2^n\). Dès que le nombre de qubits dépasse la quarantaine (et même bien avant), il devient absolument impossible en pratique de faire ce calcul avec un ordinateur classique 👎🏻.
Or il existe de nombreux domaines d’applications où on aimerait être en mesure de faire ce calcul. En effet cette équation apparait dès qu’on s’intéresse à un matériau qu’on ne peut pas décrire précisément sans la mécanique quantique. C’est souvent le cas en science des matériaux, en chimie et en biologie. Si on prend l’exemple de la chimie, la dimension du vecteur \(\vert \psi \rangle\) d’une molécule est exponentielle en son nombre d’électrons 😰. Pour une molécule ayant une cinquantaine d’électrons, on est donc obligé de recourir à des approximations violentes pour pouvoir la simuler à l’aide d’un ordinateur classique.

En revanche on peut donner une bonne expression approchée de \(\vert \psi(t) \rangle\) par Trotterisation:

\[\vert \psi (t) \rangle \approx \prod_{k = 1}^{\lfloor \frac{t}{\delta t} \rfloor} e^{\frac{\hat{H}}{i\hbar} \delta t} \, \, \vert \psi (0) \rangle\]

Cette approximation converge vers la solution exacte lorsque \(\delta t\) tend vers \(0\). De plus si on dispose d’un ordinateur quantique, on peut préparer l’état initial \(\vert \psi(0) \rangle\) sur seulement \(n\) qubits 🤩. Puis appliquer \(\lfloor \frac{t}{\delta t} \rfloor\) fois l’opération quantique \(e^{\frac{\hat{H}}{i\hbar} \delta t}\). On obtient ainsi une bonne version approchée de \(\vert \psi (t) \rangle\) (si on a choisi un \(\delta t\) suffisamment petit).

En combinant cette approche à l’algorithme quantique d’estimation de phase on peut calculer l’énergie de différents états d’un système quantique. Lorsqu’on dit que l’ordinateur quantique va permettre de trouver de nouveaux matériaux, de nouveaux médicaments et de nouvelles réactions chimiques, on pense généralement à cette approche combinant Trotterisation et estimation de phase.

Par ailleurs des techniques sophistiquées de simulation Hamiltonienne 💪 permettent de transformer le spectre (c’est-à-dire l’ensemble des valeurs propres) de l’opération quantique \(e^{\frac{\hat{H}}{i\hbar} \delta t}\). Je pense notamment à la technique de transformation quantique des valeurs singulières. Lorsque cette transformation correspond à la fonction inverse : \(\lambda \mapsto \frac{1}{\lambda}\), cela permet d’inverser une matrice de taille \(2^n\). Les algorithmes quantiques d’algèbre linéaire comme HHL reposent largement sur cette possibilité. Les applications de l’ordinateur quantique en optimisation convexe, en résolution d’équation différentielle et en machine learning quantique utilisent généralement cet outil d’algèbre linéaire quantique.

Cas d’un Hamiltonien exprimé comme une somme

Il est courant en simulation moléculaire que l’Hamiltonien total soit exprimé comme une somme d’Hamiltonien. Soit parce que chaque terme de la somme correspond à un phénomène physique différent : par exemple d’une part l’interaction entre le noyau et les électrons et d’autre part l’interaction entre électrons. Soit parce que chaque terme correspond à une zone locale de la molécule. Dans ces cas l’Hamiltonien total \(\hat{H}\) s’écrit:

\[\hat{H} = \sum_{j=1}^{m} \hat{H}_j.\]

Il est alors possible de décomposer chaque terme \(e^{\frac{\hat{H}}{i\hbar} \delta t}\) en un produit de termes:

\[e^{\frac{\hat{H}}{i\hbar} \delta t} \approx \prod_{j=1}^{m} e^{\frac{\hat{H_j}}{i\hbar} \delta t}\]

Cette décomposition est très utile dans le but d’implémenter \(e^{\frac{\hat{H}}{i\hbar} \delta t}\) sur un ordinateur quantique car on peut alors implémenter successivement chaque terme \(e^{\frac{\hat{H_j}}{i\hbar} \delta t}\). Cela revient à implémenter le produit de ces termes. Or typiquement, chaque terme \(e^{\frac{\hat{H_j}}{i\hbar} \delta t}\) ne fait intervenir qu’un petit sous-ensemble de l’ensemble des qubits sur lesquels \(e^{\frac{\hat{H}}{i\hbar} \delta t}\) agit ✂️. Il est donc bien plus facile d’implémenter \(e^{\frac{\hat{H_j}}{i\hbar} \delta t}\) que d’implémenter \(e^{\frac{\hat{H}}{i\hbar} \delta t}\).

Cette approximation n’en serait pas une (elle serait exacte) dans le problème simplifié que j’ai introduit précédemment : si \(\alpha = \sum_{j=1}^{m} \alpha_j\), alors

\[e^{\alpha \delta t} = \prod_{j=1}^{m} e^{\alpha_j \delta t}.\]

Dans le cas d’un Hamiltonien \(\hat{H}\), c’est une approximation car les \(\hat{H}_j\) ne commutent pas : \(\hat{H}_j \hat{H}_k \neq \hat{H}_k \hat{H}_j\) en général. Pour réduire l’erreur commise par cette décomposition, on peut utiliser l’une des formules de Trotter-Suzuki 🏍️. En fonction du degré de précision souhaité, on utilisera une formule de Trotter-Suzuki plus ou moins sophistiquée. J’ai donné ci-dessus la formule de Trotter-Suzuki du premier ordre. La librairie de chimie de Q# permet d’utiliser facilement une formule de Trotter-Suzuki de l’ordre souhaité. Dans l’exemple suivant qSharpData encode les différents termes \(\hat{H}_j\) de l’Hamiltonien qu’on veut simuler. En quelques lignes de code, on implémente la formule de Trotter-Suzuki d’ordre 4 :

Les formules de Trotter-Suzuki d’ordre au moins égal à 2 combinent astucieusement les approximations faites en temps (\(e^{\frac{\hat{H}}{i\hbar} t} \approx \prod_{k = 1}^{\lfloor \frac{t}{\delta t} \rfloor} e^{\frac{\hat{H}}{i\hbar} \delta t}\)) et en espace (\(e^{\frac{\hat{H}}{i\hbar} \delta t} \approx \prod_{j=1}^{m} e^{\frac{\hat{H_j}}{i\hbar} \delta t}\)) : à chaque pas de temps les termes d’espace \(e^{\frac{\hat{H_j}}{i\hbar} \delta t}\) apparaissent dans un ordre différent. Cela permet de minimiser l’erreur d’approximation totale. Plus l’ordre d’une formule de Trotter-Suzuki est grand, plus l’erreur commise est petite mais plus son temps d’exécution sur un ordinateur quantique est grand.

Conclusion

La Trotterisation n’est rien de plus qu’une méthode numérique de résolution d’une équation différentielle du premier ordre : l’équation de Schrödinger.

Implémenter l’opération \(e^{\frac{\hat{H}}{i\hbar} t}\) sur un ordinateur quantique demande une quantité de mémoire quantique exponentiellement plus faible que la quantité de mémoire classique nécessaire sur un ordinateur classique.

Cette obervation est à l’origine de nombreuses applications de l’ordinateur quantique. L’ensemble des outils ingénieux permettant d’implémenter cette opération sur un ordinateur quantique forme le domaine de la simulation Hamiltonienne.