Chimie quantique

Prenons l’exemple d’une réaction produisant du méthanol à partir de dioxyde de carbone. L’intérêt à réaliser cette réaction chimique est bien entendu immense dans le cadre de la lutte contre le réchauffement climatique.

\[CO_2 + 3 H_2 \rightarrow CH_3 OH + H_2 0\]

Pour que cette réaction ait lieu, il ne suffit pas de mettre en contact du dioxyde de carbone et du dihydrogène. Il faut également mettre aux contacts de ces réactifs un catalyseur. La question est de trouver ce catalyseur. Une approche consiste à tester un grand nombre de candidats catalyseurs en laboratoire. C’est l’approche in vitro. Une alternative est de faire un premier tri parmi les catalyseurs in silico, c’est-à-dire à l’aide d’ordinateurs classiques et de méthodes de chimie computationnelle. Une troisième approche consiste à utiliser, en plus de méthodes classiques, un ordinateur quantique pour réaliser ces calculs. J’ai envie de parler d’approche in qubito. Dès qu’on saura de quels matériaux seront faits les ordinateurs quantiques tolérants aux fautes et de grande taille, on pourra trouver un meilleur nom que in qubito pour cette approche utilisant un ordinateur quantique 🙂.

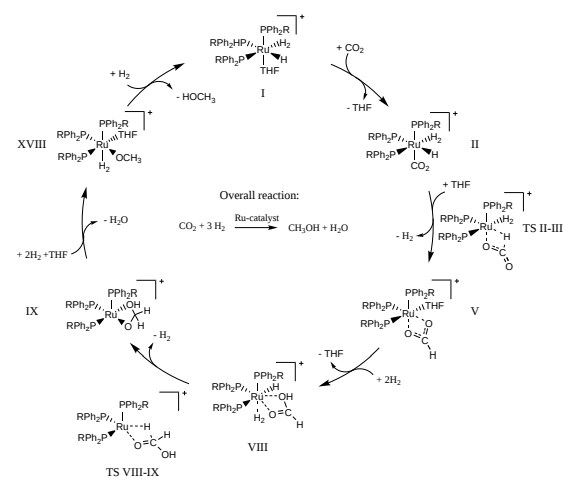
L’équation de la réaction chimique ci-dessus est en fait un résumé de ce qu’il se passe vraiment. Lorsqu’on s’intéresse au mécanisme réactionnel, on se rend compte que les réactifs (dioxyde de carbone et dihydrogène) passent par des étapes intermédiaires avant de devenir les produits (méthanol et eau). C’est particulièrement vrai pour une réaction utilisant un catalyseur : dans les détails, le catalyseur est transformé au cours de la réaction. Le catalyseur n’intervient pas dans l’équation bilan car sa transformation est circulaire. En d’autres termes son état initial est identique à son état final.

source pour l’image: Quantum computing enhanced computational catalysis

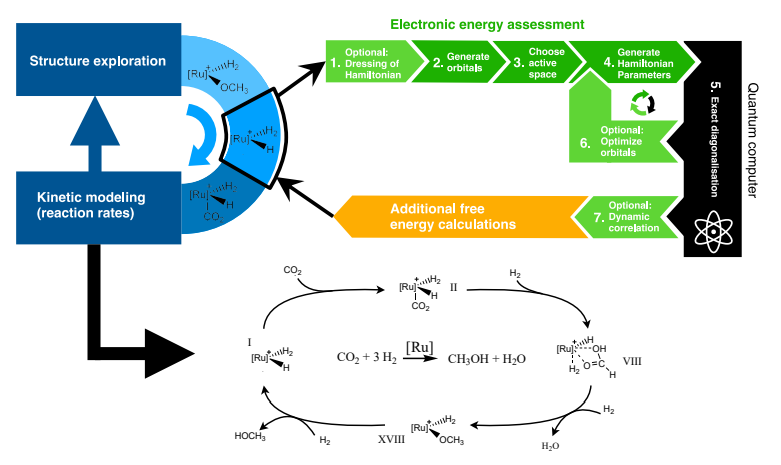
Pour comprendre la vitesse à laquelle a lieu chaque étape élémentaire du mécanisme réactionnel, on a besoin de connaitre les différences d’énergie (ou plus précisément d’énergie libre) de l’ensemble des composants chimiques à trois moments : avant l’étape élémentaire, au moment où l’énergie est maximale et après l’étape élémentaire. Si on dispose de ces informations, on peut en déduire à l’aide d’un modèle cinétique l’effet du candidat catalyseur sur la réaction chimique. Selon les résultats on teste le catalyseur en laboratoire ou on explore d’autres structures numériquement.

source pour l’image: Quantum computing enhanced computational catalysis

L’ordinateur quantique n’intervient que dans une partie petite (mais cruciale) de ce processus. Il permet de calculer l’énergie de différents composés chimiques qui interviennent au cours de cette réaction. Etant donné que la valeur de ces énergies peut dépendre fortement d’effets quantiques, il n’est pas surprenant que l’ordinateur quantique puisse apporter un avantage par rapport aux méthodes classiques de chimie computationnelle qui permettent de réaliser ces calculs d’énergie. Avant de donner quelques détails sur les algorithmes quantiques envisagés, j’aimerais rappeler la façon dont on modélise une molécule entourée de son nuage d’électrons.

Fermions et deuxième quantification

L’espace utilisé pour décrire l’état de chaque électron d’une molécule est absolument gigantesque : c’est un espace de dimension infinie. Pour donner un point de comparaison, l’espace utilisé pour décrire un qubit est de dimension 2 car tout état d’un qubit peut être décrit comme une combinaison linéaire de l’état \(\vert 0 \rangle\) et de l’état \(\vert 1 \rangle\). L’ensemble des états que peut prendre un qubit est tout de même infini, mais c’est une infinité de dimension 2. Pour un électron on a affaire à une infinité de dimension infinie.

Néanmoins un électron d’une molécule a tendance à rester proche de cette molécule. Une grosse partie de la fonction d’onde d’un électron peut donc être exprimée comme une combinaison linéaire d’un nombre fini d’éléments de base. La fonction d’onde d’un électron est la description mathématique de son état. Chaque élément de base est appelé une orbitale. Il est courant de se limiter à des combinaisons linéaires de \(L\) orbitales pour décrire la fonction d’onde d’un électron. Si \(L\) est suffisamment grand et qu’on a bien choisi les orbitales, on parvient ainsi à décrire \(99,9999 \%\) (par exemple) de la vraie fonction d’onde de l’électron.

Une fois qu’on a choisi une base de \(L\) orbitales, il n’est plus nécessaire d’utiliser les 3 dimensions d’espace pour décrire la fonction d’onde d’un électron. Il suffit de décrire la combinaison linéaire d’orbitales occupées par cet électron. Si on voulait retrouver la fonction d’onde spatiale de cet état de l’électron, on pourrait utiliser la description spatiale de chaque orbitale. On parle de deuxième quantification lorsqu’on a choisi une base d’orbitales et qu’on ne parle plus qu’en termes d’occupation d’orbitales par les électrons. A l’inverse, la première quantification fait référence à la description spatiale des fonctions d’onde des électrons.

De plus les différents électrons d’une molécule sont indistinguables : la situation où l’électron \(1\) occupe l’orbitale \(a\) et l’électron \(2\) occupe l’orbitale \(b\) est rigoureusement identique à celle où l’électron \(1\) occupe l’orbitale \(b\) et l’électron \(2\) occupe l’orbitale \(a\). A cause de cette symétrie, des particules indistinguables peuvent être ou bien des bosons ou bien des fermions. Il se trouve que les électrons sont des fermions. Concrètement cela veut dire que la fonction d’onde de deux électrons doit être multipliée par \(-1\) lorsqu’on échange les rôles de deux électrons. Encore plus concrètement cela veut dire qu’une même orbitale ne peut être occupée que par au plus un électron. Ce résultat est également connu sous le nom de principe d’exclusion de Pauli. Pour bien comprendre, prenons l’exemple de 2 électrons dans un espace de 3 orbitales, notées \(a\), \(b\) et \(c\). L’état où l’électron \(1\) occupe l’orbitale \(a\) et l’électron \(2\) occupe l’orbitale \(b\) peut être noté \(\vert a b \rangle\). Mais cet état n’est pas licite pour des fermions. En effet si on échange les rôles des électrons \(1\) et \(2\), on obtient l’état \(\vert b a \rangle\) qui n’est pas égal à \(- \vert a b \rangle\) comme ça devrait être le cas pour des fermions. En fait la fonction d’onde (non normalisée) qui permet de représenter la configuration où les orbitales \(a\) et \(b\) sont occupées par les électrons \(1\) et \(2\) est la suivante :

\[\vert a b \rangle - \vert b a \rangle\]

Cette fois-ci, échanger les positions des électrons 1 et 2 correspond bien à multiplier globalement la fonction d’onde par \(-1\).

De façon plus générale, pour \(N\) électrons occupant \(N\) orbitales, il existe une seule fonction d’onde respectant les statistiques d’échange de fermions (multiplication de la fonction d’onde par \(-1\) lorsqu’on échange le rôle de deux électrons). Il s’agit d’une somme des \(N!\) permutations des \(N\) électrons au sein des \(N\) orbitales occupées avec un coefficient \(+1\) devant la moitié des permutations et un coefficient \(-1\) devant l’autre moitié des permutations. Comme cette somme peut être exprimée de façon compacte comme un déterminant, on parle de déterminant de Slater. Comme il est fastidieux d’écrire une somme de \(N!\) termes, on préfère généralement donner l’ensemble de \(N\) orbitales occupée par les \(N\) électrons. Il faut comprendre que l’ordre dans lequel on liste ces \(N\) orbitales occupées n’a pas d’importance. On parle alors d’une configuration de \(N\) électrons.

Peut-on toujours décrire l’état de \(N\) électrons dans une base de \(L\) orbitales en donnant une seule configuration (i.e. un seul déterminant de Slater) ? Pas exactement, non : il ne faut pas oublier qu’en mécanique quantique, on peut toujours considérer des superpositions d’état. Ici, on va donc considérer des superpositions (i.e. des combinaisons linéaires) de configurations de \(N\) électrons. Comme il existe \(L \choose N\) façon de choisir \(N\) orbitales occupées parmi \(L\) orbitales, on représente l’ensemble des états possibles de \(N\) électrons restreints à \(L\) orbitales par un espace vectoriel de dimension \(L \choose N\). La base canonique de cet espace vectoriel est paramétrée par les \(L \choose N\) façons de choisir \(N\) orbitales occupées parmi \(L\) orbitales.

Il reste une difficulté à résoudre avant d’utiliser des qubits pour représenter cet espace vectoriel : les qubits ne sont pas des fermions, on peut plutôt considérer que ce sont des particules distinguables. En effet on sait différencier le qubit 1 du qubit 2, ne serait-ce que parce qu’ils se trouvent physiquement à des endroits différents. Un espace vectoriel de qubits n’a donc pas la même structure qu’un espace vectoriel de fermions. Heureusement, on sait plonger un espace vectoriel de fermions à l’intérieur d’un espace vectoriel de qubits. On utilise pour cela des représentations comme celle de Jordan-Wigner ou celle de Bravyi-Kitaev. Equipés d’une de ces transformations, nous pouvons maintenant réaliser le calcul d’énergie qui nous intéresse à l’aide d’un ordinateur quantique.

Un algorithme quantique en 3 parties

L’approche la plus prometteuse pour réaliser un calcul d’énergie (d’une molécule ou d’une structure crystalline) à l’aide d’un ordinateur quantique peut être décomposée en 3 parties :

1. Préparation d’un état quantique proche de l’état fondamental.
2. Simulation Hamiltonienne.
3. Estimation de phase.

 

Estimation de phase

L’estimation de phase permet d’estimer la valeur propre \(\lambda\) d’une porte quantique \(U\) si on dispose du vecteur propre associé \(\vert \psi \rangle\) :

\[U \vert \psi \rangle = \lambda \vert \psi \rangle\]

Si on parvient à synthétiser la porte \(U\) correspondant à la dynamique de la molécule (\(e^{ -\frac{i \hat{H} t}{\bar{h}} }\)) par simulation Hamiltonienne et à préparer l’état fondamental \(\psi_0\) de cette molécule alors le \(\lambda\) estimé est égal à \(e^{ -\frac{i E_0 t}{\bar{h}} }\). Une estimation de \(\lambda\) fournit ainsi une estimation de \(E_0\), l’énergie fondamentale recherchée.

Les deux prochaines sections décrivent des approches pour préparer l’état fondamental \(\psi_0\) et pour synthétiser cette porte \(U\).

Préparation d’un état quantique proche de l’état fondamental

Il n’est pas indispensable de préparer exactement l’état fondamental \(\psi_0\) de l’Hamiltonien de la molécule qui nous intéresse. Il suffit de préparer un état \(\psi_{trial}\) qui en soit suffisamment proche. En effet si on réalise un algorithme quantique d’estimation de phase en remplaçant \(\psi_0\) par \(\psi_{trial}\), on obtient le bon résultat (i.e. celui qu’on aurait obtenu avec \(\psi_0\)) avec une probabilité de succès égal à

\[p_{succès} = \vert \langle \psi_0 \vert \psi_{trial} \rangle \vert^2.\]

Si \(p_{succès}\) n’est pas nulle, il est possible de répéter l’opération un nombre de fois suffisamment grand pour avoir une probabilité de succès arbitrairement proche de \(1\).

Une approche fructueuse pour préparer un état quantique proche de l’état fondamental consiste à se limiter aux \(L \choose N\) états de la base de l’espace des \(N\) électrons parmi \(L\) orbitales. L’état d’énergie minimale parmi cet ensemble s’appelle l’état de Hartree-Fock et il existe des méthodes classiques (i.e. utilisant des ordinateurs classiques) efficaces pour approximer cet état. Il existe également des méthodes classiques dites post-Hartree-Fock permettant potentiellement de trouver un état quantique plus proche de l’état fondamental que l’état de Hartree-Fock. Une fois qu’on a obtenu par une de ces méthodes la description d’un état quantique proche de l’état fondamental, on prépare cet état quantique à l’aide de portes quantiques élémentaires.

Une alternative consiste à obtenir directement un état quantique proche de l’état fondamental en utilisant un ordinateur quantique. L’algorithme VQE (Variational Quantum Eigensolver) consiste à préparer un état quantique sous la forme d’un circuit paramétré et à estimer l’énergie moyenne de cet état quantique. Cette énergie moyenne est ensuite utilisée pour optimiser les paramètres du circuit quantique de façon à préparer un état quantique d’énergie moyenne la plus basse possible. L’algorithme VQE est particulièrement populaire en ce moment parce qu’il peut être implémenté sur des ordinateurs quantiques NISQ (Noisy Intermediate Scale Quantum device), c’est-à-dire des ordinateurs quantiques non tolérants aux fautes.

Simulation Hamiltonienne

Au sein des 3 parties de l’approche quantique, la simulation Hamiltonienne est le domaine où la recherche est aujourd’hui la plus active. Etant donné une description de l’Hamiltonien \(H\) de la molécule qui nous intéresse, le but est de synthétiser une opération quantique \(U\) qui correspond à l’évolution selon l’équation de Schrödinger pendant un temps \(t\) :

\[U = e^{ -\frac{i \hat{H} t}{\bar{h}} }\]

Il existe de nombreuses approches pour approximer cette évolution. La plus ancienne et la plus intuitive consiste à discrétiser en temps et à trouver des approximations habiles de l’évolution pendant un petit pas de temps : on parle de Trotterisation. C’est cette approche qui a été retenue dans l’article Elucidating Reaction Mechanisms on Quantum Computers pour estimer les ressources nécessaires à la simulation d’un catalyseur de la fixation de l’ammoniac.

Depuis 2016, la qubitisation offre une alternative efficace et flexible. Aujourd’hui les approches les plus efficaces consistent à utiliser la qubitisation sur une représentation compacte de l’Hamiltonien qui nous intéresse. L’article Qubitization of Arbitrary Basis Quantum Chemistry Leveraging Sparsity and Low Rank Factorization met à profit les symétries d’un Hamiltonien fermionique pour le factoriser. L’article Quantum computing enhanced computational catalysis propose une double factorisation de l’Hamiltonien pour réduire encore les ressources quantiques nécessaires.

Conclusion

Aujourd’hui les algorithmes quantiques de chimie nécessitent quelques milliers de qubits logiques et quelques milliards de portes quantiques non-Clifford. Il est courant de compter la complexité d’un algorithme quantique tolérant aux fautes en portes non-Clifford car ce sont de très loin les portes quantiques les plus coûteuses à implémenter sur les architectures tolérantes aux fautes les plus prometteuses aujourd’hui.

Bien que le hardware quantique d’aujourd’hui ne propose pas des ressources quantiques en nombre aussi important, il est extrêmement encourageant de voir la vitesse à laquelle les progrès en algorithmique quantique font diminuer les ressources requises.

L’avènement de l’ordinateur quantique pour la chimie quantique aura lieu lorsque la courbe croissante des progrès du hardware quantique viendra croiser la courbe décroissante des ressources nécessaires. Etant donné l’importance des cas d’usage de la chimie quantique, j’ai hâte de voir ce jour arriver !