Comment réduire le coût d'un programme quantique?

Les ordinateurs quantiques d’aujourd’hui (décembre 2020) ont un nombre de qubits généralement inférieur à 50 et le nombre d’opérations quantiques qu’ils peuvent appliquer à ces qubits est de l’ordre de quelques dizaines. Même si ces caractéristiques vont probablement énormément progresser dans les années à venir, il est essentiel lorsqu’on écrit un programme quantique d’optimiser les ressources (nombre de qubits et nombre d’opérations quantiques) utilisées par ce programme. Je prends ici l’exemple d’une opération quantique souvent utilisée dans l’algorithme quantique de recherche de Grover et j’utilise quelques outils du Quantum Development Kit.

L’algorithme de Grover permet de trouver rapidement un objet parmi un grand nombre d’objets. Disons par exemple qu’on dispose de \(1024\) objets et que l’un d’entre eux est marqué, c’est-à-dire que c’est l’objet qu’on cherche à identifier. Comme \(2^{10} = 1024\), on peut utiliser \(10\) bits pour indexer les \(1024\) objets.

Supposons par exemple que l’objet marqué est celui qui est indexé par \(1111111111\). C’est le moment de préciser ce que je veux dire par objet marqué : ici nous voulons utiliser ce marquage dans l’algorithme quantique de Grover. Il faut donc que le marquage soit lui-même quantique. Plus précisément on va utiliser \(10\) qubits (de même qu’on aurait utilisé \(10\) bits si on se servait de mémoire classique) pour indexer les \(1024\) objets. Le marquage est une opération quantique qui laisse les \(1023\) états différents de l’état \(\vert 1111111111 \rangle\) inchangés et qui change \(\vert 1111111111 \rangle\) en \(- \vert 1111111111 \rangle\).

Le symbole \(\vert \, \, \rangle\) (prononcer “ket”) permet de différencier la mémoire quantique (les qubits) de la mémoire classique. Pour comprendre ce que signifie le signe “moins” devant l’état d’un qubit, je vous renvoie vers ce billet de blog. Dans le jargon de l’algorithmique quantique, on parle d’oracle à phase pour désigner cette opération quantique de marquage.

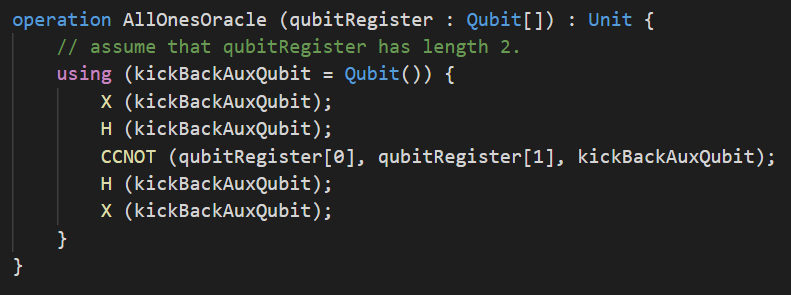
Pour prendre le temps d’introduire les concepts au fur et à mesure 🚀, nous allons d’abord traiter le cas d’un registre de \(2\) qubits plutôt que celui d’un registre de \(10\) qubits. Voici une implémentation en Q# de l’oracle qui marque l’état \(\vert 11 \rangle\):

L’opération quantique AllOnesOracle prend comme argument le tableau de qubits qubitRegister. Ici on suppose que ce tableau est de longueur 2. Comme AllOnesOracle ne renvoie rien, son type de sortie est Unit. AllOnesOracle utilise un qubit auxiliaire : kickBackAuxQubit. Cette implémentation de AllOnesOracle utilise la technique du retour de phase pour transformer un oracle à qubit auxiliaire en un oracle à phase. Si vous n’avez pas lu mon billet de blog sur le retour de phase, vous risquez de ne pas comprendre cette implémentation de AllOnesOracle mais ça ne devrait pas vous empêcher de comprendre la suite sur l’estimation de ressources quantiques 🤞.

La porte \(CCNOT\) (également appelée porte de Toffoli) applique une porte \(NOT\) au qubit auxiliaire si et seulement si les deux qubits de qubitRegister sont tous deux dans l’état \(\vert 1 \rangle\). La porte \(CCNOT\) implémente donc AllOnesOracle sous la forme d’un oracle à qubit auxiliaire. Les portes \(X\) et \(H\) appliquées avant et après cette opération sont la façon standard de transformer un oracle à qubit auxiliaire en un oracle à phase.

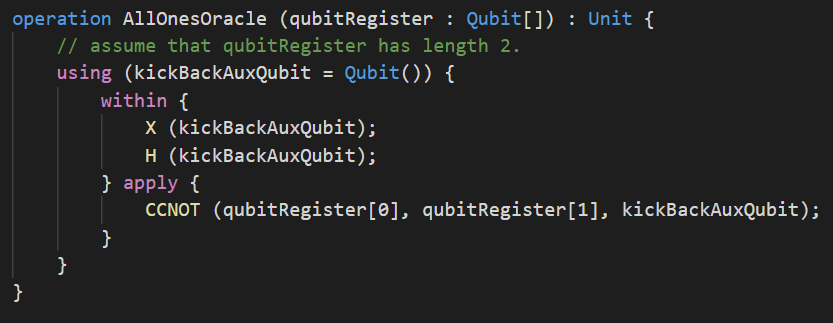
Appliquer une opération quantique (ici les portes \(X\) et \(H\)) avant et après une autre opération quantique (ici la porte \(CCNOT\)) est un procédé très courant en programmation quantique. En mathématiques, on dit qu’on conjugue l’opération \(CCNOT\) par les opérations \(X\) et \(H\). Le langage Q# a une syntaxe permettant d’exprimer une conjugaison de façon concise :

Le compilateur Q# comprend ici que le bloc “within” (c’est-à-dire les portes \(X\) et \(H\)) doit être appliqué une fois avant le bloc “apply” (c’est-à-dire la porte \(CCNOT\)) et une deuxième fois dans l’autre sens après le bloc “apply”. La syntaxe “within - apply” rend un programme plus lisible car elle correspond à la façon dont un programmeur quantique pense à son programme (en tout cas en ce qui me concerne).

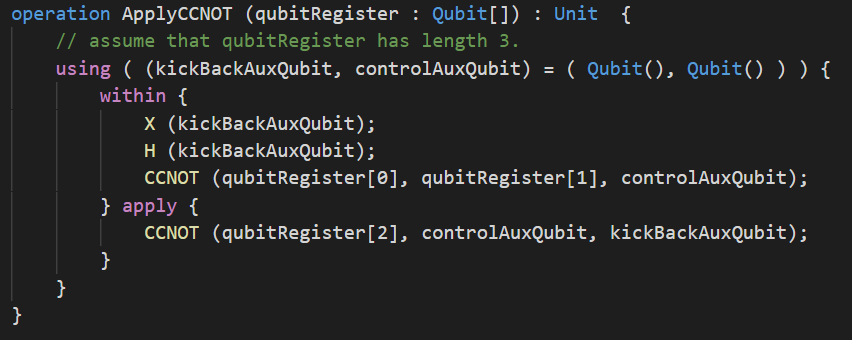
Si maintenant qubitRegister est constitué de 3 qubits au lieu de 2, on aimerait écrire le même programme en remplaçant la porte \(CCNOT\) par une porte \(CCCNOT\) qui change la valeur du qubit auxiliaire si et seulement si les 3 qubits de qubitRegister sont dans l’état \(\vert 1 \rangle\). Sauf que la porte \(CCCNOT\) n’existe pas en Q# 😄. On peut s’en sortir en utilisant un qubit auxiliaire supplémentaire :

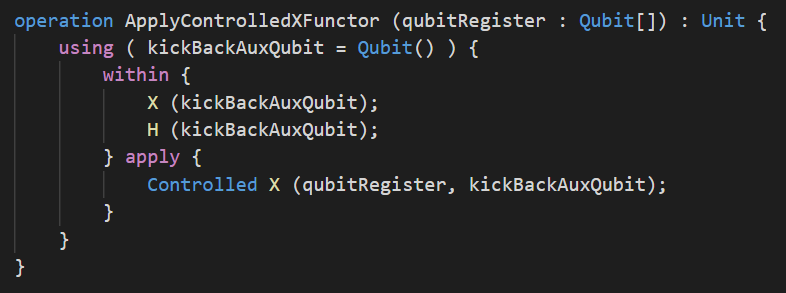
Quelque soit le nombre de qubits contenus par qubitRegister, on peut s’en sortir ainsi : il suffit d’utiliser un qubit auxiliaire supplémentaire pour chaque qubit supplémentaire de qubitRegister. Toutefois devoir gérer manuellement la déclaration des qubits auxiliaires peut être fastidieux pour le programmeur Q#. Heureusement on peut également utiliser le foncteur Controlled qui permet de contrôler une opération quantique sur un nombre arbitraire de qubits. Ainsi Controlled X (qubitRegister, kickBackAuxQubit) est l’équivalent de ce que serait C...CNOT (qubitRegister[0], ..., qubitRegister[n-1], kickBackAuxQubit) si la porte \(C...CNOT\) avec n \(C\) existait! Voici l’oracle AllOnesOracle implémenté pour un nombre arbitraire de qubits :

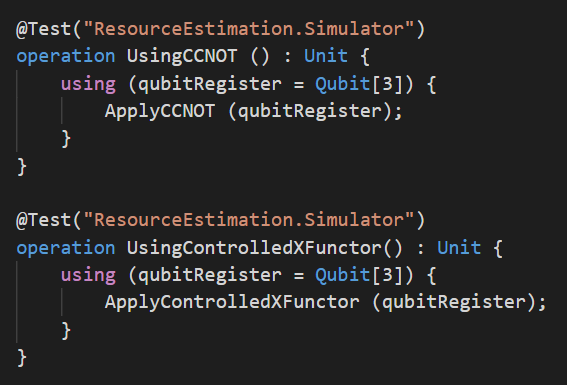
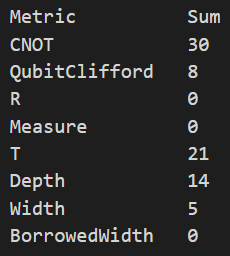
On a donc deux implémentations différentes de la même opération quantique. Quelle implémentation est la plus efficace ? On peut utiliser le ResourceEstimation.Simulator de Q# pour répondre à cette question :

Les résultats obtenus dans les deux cas sont strictement identiques. En fait il se trouve que l’implémentation par le langage Q# du foncteur Controlled correspond exactement à ce que je fais à la main en introduisant le qubit auxiliaire controlAuxQubit dans l’opération ApplyCCNOT.

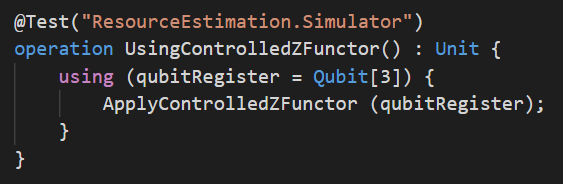
Il existe une troisième façon d’implémenter AllOnesOracle, que personnellement je trouve un peu moins naturelle. On peut remarquer que la porte quantique \(Z\) applique une phase \(-1\) à l’état \(\vert 1 \rangle\) d’un qubit mais pas à son état \(\vert 0 \rangle\). En contrôlant sur tous les qubits de qubitRegister sauf l’un d’entre eux et en appliquant une porte \(Z\) à ce dernier qubit, on obtient l’opération AllOnesOracle:

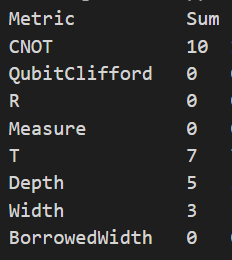
Cette implémentation est rendue particulièrement concise par l’utilisation des fonctions Q# Most et Tail du namespace “Microsoft.Quantum.Arrays” de la bibliothèque standard de Q#. Ces deux fonctions prennent un Array en argument. Most renvoie un Array contenant tous les éléments sauf le dernier et Tail renvoie le dernier élément. Quelles sont les ressources utilisées par cette implémentation ?

On voit que cette implémentation réduit d’un facteur 3 le nombre de portes \(T\) requises. Cette métrique est très importante car appliquer une porte \(T\) est de très loin la ressource la plus coûteuse pour un ordinateur quantique tolérant aux fautes (c’est-à-dire utilisant de la correction d’erreur quantique). On voit également que le nombre de qubits (Width) passe de 5 à 3 et que la profondeur (Depth) passe de 14 à 5.

Par défaut avec l’estimateur de ressources de Q#, la profondeur donnée est en fait la profondeur en portes \(T\). C’est-à-dire le nombre de pas de temps pendant lesquels on applique une porte \(T\) à au moins un qubit. En effet comme une porte \(T\) tolérante aux fautes prend bien plus de temps à exécuter que les autres portes (de Clifford), la profondeur en porte \(T\) est quasiment proportionnelle au temps d’exécution tolérante aux fautes d’une opération quantique.
Pour un ordinateur quantique n’utilisant pas de correction d’erreur, le temps d’exécution d’une opération quantique est proportionnel à la profondeur toutes portes confondues. On peut également paramétrer l’estimateur de ressources de Q# pour qu’il renvoie la profondeur toutes portes confondues.

Conclusion

Les ressources quantiques (qubits et opérations appliquées à ces qubits) sont aujourd’hui extrêmement rares. Dans les années à venir, ces ressources vont certainement devenir nettement plus abondantes. Néanmoins, pendant encore au moins une vingtaine d’années à mon avis, il sera absolument indispensable d’optimiser l’utilisation qu’on fait de ces ressources pour implémenter chaque opération quantique d’un programme. L’estimateur de ressource de Q# est un outil précieux pour trouver ces implémentations optimales.

Nous nous sommes intéressés dans ce billet de blog à une opération quantique relativement simple. En revanche un programme quantique permettant de donner des réponses auxquelles nous n’avons pas accès avec des ordinateurs classiques sera sans aucun doute bien plus complexe 🤯.
Le hardware quantique actuel ne permet pas encore d’exécuter un tel programme quantique. Mais on peut dès aujourd’hui le développer, estimer les ressources quantiques qu’il requiert et en donner une implémentation optimisée. En effet contrairement à un simulateur d’état quantique, l’estimateur de ressources quantiques ne donne pas le résultat d’un calcul quantique. En contrepartie il n’est pas soumis aux limites des simulateurs d’état quantique : il est possible d’estimer les ressources requises par un programme utilisant plusieurs milliers de qubits et de profondeur arbitrairement grande.