Amplification d'amplitude

Qu’est-ce qui est plus grand : \(\epsilon\) ou \(\sqrt{\epsilon}\) ? En prenant comme exemple \(\epsilon = 0.01\) et donc \(\sqrt{\epsilon} = 0.1\), on se rend facilement compte que \(\sqrt{\epsilon}\) est plus grand que \(\epsilon\) pour les petites valeurs.
Par ailleurs l’information est encodée dans de la mémoire quantique par des amplitudes de probabilité qui sont des racines carrées de probabilités.

Le problème de la recherche non structurée

Le problème auquel on va s’intéresser dans ce billet de blog est celui de la recherche non structurée : parmi \(2^n\) éléments, un seul d’entre eux est “marqué”. Il s’agit de retrouver cet élément alors qu’on n’a aucune information supplémentaire : il n’y a pas de structure particulière sur cet ensemble de \(2^n\) éléments. On jugera de l’efficacité d’une méthode en fonction du nombre d’éléments qu’on aura “testés” avant de trouver l’élément “marqué”. Si on ne dispose pas d’ordinateur quantique, il n’y a pas moyen de faire mieux que ce que je fais lorsque je cherche la clé de chez moi dans le noir : j’essaie toutes les clés jusqu’à ce que je tombe sur la bonne ! Si j’ai \(2^n\) clés sur mon trousseau, à chaque nouvel essai j’ai de l’ordre de \(\epsilon = \frac{1}{2^n}\) chances de tomber sur la bonne clé. Il me faudra donc de l’ordre de \(2^n\) essais avant de rentrer chez moi (en moyenne \(2^{n-1}\) essais). Dit autrement, ma probabilité de succès augmente d’environ \(\epsilon\) à chaque essai.

Une spécificité du calcul quantique est de manipuler des amplitudes de probabilité. C’est-à-dire des nombres dont le carré correspond à une probabilité.

Formalisons notre problème de recherche non structurée : finis les trousseaux de clé, nous allons maintenant parler d’indices, de fonctions booléennes et d’oracles 😊. On considère donc l’ensemble \(\{0, 1\}^n\) (le trousseau de clé) et une fonction \(f : \{0, 1\}^n \rightarrow \{0, 1\}\). \(f\) est la fonction de “marquage” : parmi ses \(2^n\) inputs, elle renvoie \(1\) sur un seul d’entre eux (la bonne clé) ! Pour fixer les idées, on peut imaginer que \(n=10\) est que l’élément marqué est \(0010111101\). \(f\) renvoie \(0\) sur les \(2^n - 1\) autres éléments (les clés inutiles du trousseau). Comme on ne sait pas comment cette fonction \(f\) a été inventée (ni par qui d’ailleurs), on lui donne parfois le nom d’oracle : c’est pour nous une boite noire qui nous fournit un output (\(0\) ou \(1\)) à chaque fois qu’on lui donne un input (comme \(1100011011\) ou \(0011011010\)).

En fait on ne rencontre pas le problème de recherche non structurée si souvent que ça. Beaucoup moins souvent que le problème de recherche structurée. Par exemple si je veux retrouver la page 114 de mon livre de 500 pages, je peux ouvrir mon livre au hasard et chercher plus à gauche lorsque je tombe sur un numéro de page supérieur à 114 et plus à droite sinon. Il s’agit d’une recherche structurée. Si je m’y prends bien, je peux trouver ma page en en testant bien moins de 500. La recherche d’un objet dans une base de données ou d’un mot dans un dictionnaire sont des recherches structurées qui ne nous intéressent pas ici.

Généralement une recherche non structurée ne se fait pas sur un ensemble concret d’objets (comme des clés) qu’on peut lister mais sur un espace abstrait de paramètres. Par exemple on veut fixer l’emploi du temps du personnel d’un hôpital. A chaque heure, chaque soignant peut travailler ou non. Pour une journée (24 heures) et 100 soignants il y a donc \(2^{2400}\) possibilités (c’est-à-dire beaucoup : un 1 suivi de 720 zéros environ). Dans cet exemple, la fonction \(f\) renvoie \(1\) si un emploi du temps satisfait toutes les contraintes (réglementaires et préférences personnelles disons) et elle renvoie \(0\) sinon.
Toutefois ce problème de recherche du bon emploi du temps est également structuré puisqu’on peut éliminer de nombreux emplois du temps en testant une seule condition. Par exemple savoir qu’un certain soignant ne peut pas travailler à 22h le mardi élimine tous les emplois du temps correspondants. En revanche savoir qu’une clé n’est pas la bonne ne nous donnait aucune information sur les autres clés.

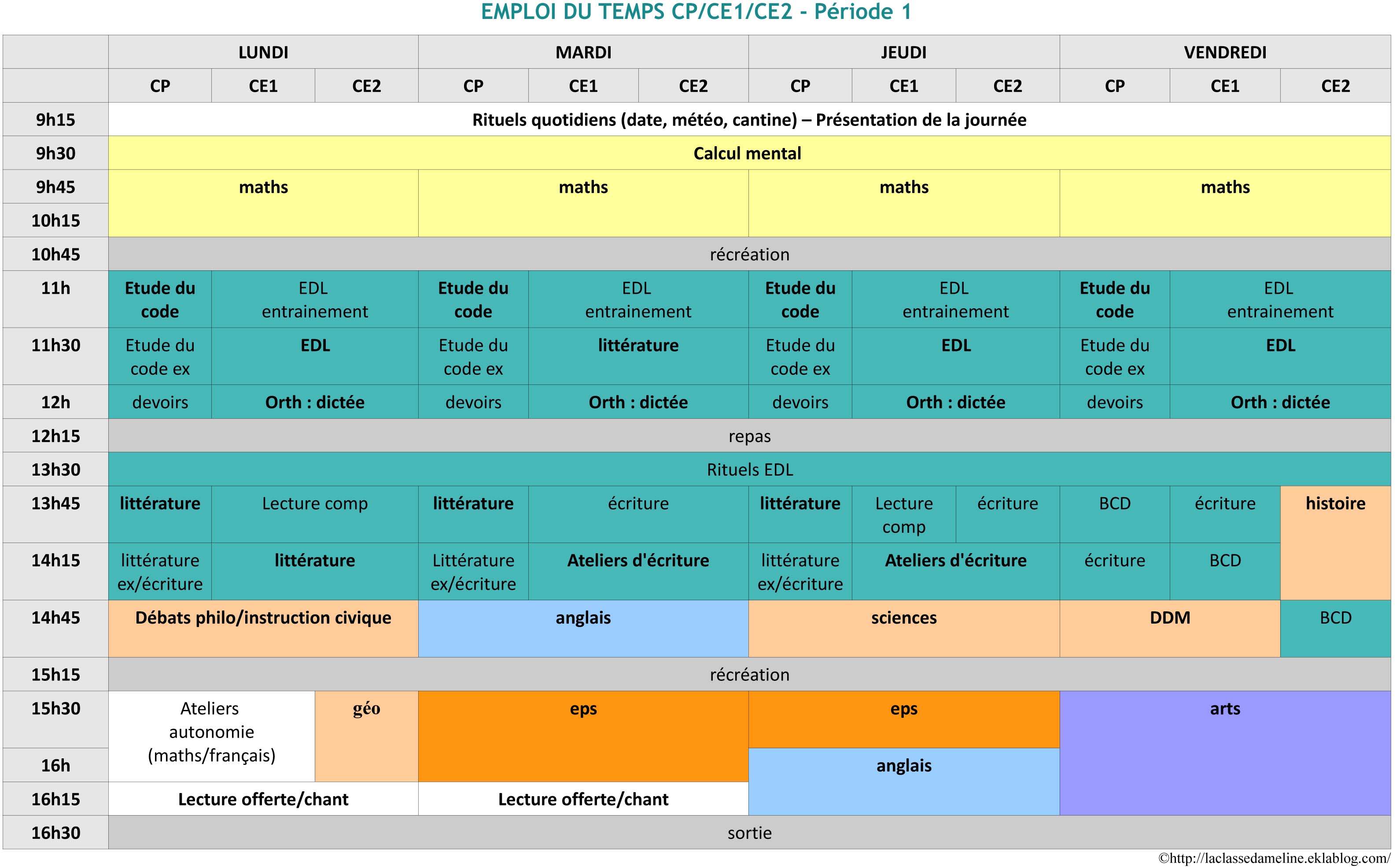
Il est toujours possible pour un problème structuré comme celui des emplois du temps de ne pas tenir compte de sa structure et de le résoudre directement par amplification d’amplitude quantique. L’amplification d’amplitude fournit donc un outil toujours disponible. De nombreux algorithmes quantiques consistent à appliquer l’amplification d’amplitude à un sous-problème du problème général.

Le modèle de calcul quantique

Quand on cherche à résoudre le problème de recherche non structurée avec un ordinateur quantique, on suppose qu’on a une version quantique de la fonction \(f\). Généralement il s’agit d’un oracle à qubit auxiliaire, comme décrit dans ce billet de blog. L’oracle à qubit auxiliaire \(U_f\) est une opération quantique qui agit sur \(n+1\) qubits : \(n\) qubits correspondant aux \(n\) bits d’input de la fonction \(f\) . \(U_f\) laisse l’état de ces \(n\) qubits inchangé. Et \(1\) qubit correspondant au bit d’output de la fonction \(f\). \(U_f\) modifie l’état de ce qubit en fonction de l’état des qubits d’input et de la même manière que \(f\) le ferait sur des bits.
Pour évaluer l’efficacité d’un algorithme quantique, on compte le nombre de fois qu’on applique l’opération \(U_f\) pour trouver l’état marqué (celui pour lequel \(f\) renvoie \(1\)). De façon cruciale, il est possible d’appliquer \(U_f\) à des états quantiques de superposition. Dans ce cas le qubit d’output va enregistrer de l’information sur \(f(x)\) pour chaque \(x\) ayant un poids non nul dans la superposition des qubits d’inputs.

Un état intéressant des qubits d’input est l’état de superposition uniforme:

\[\vert s \rangle = \frac{1}{\sqrt{2^n}} \sum_{x=0}^{2^n - 1} \vert x \rangle\]

Je sous-entends ici que les entiers naturels sont représentés en binaire. Par exemple pour \(n=10\) qubits, je note \(\vert 6 \rangle\), l’état \(0000000110\). En effet \(6 = 1 \times 4 + 1 \times 2 + 0 \times 1\). L’état de superposition uniforme a la même amplitude de probabilité (\(\frac{1}{\sqrt{2^n}}\)) devant chaque input \(x\). Il a donc le même poids devant chaque clé.

L’état marqué est l’un des \(2^n\) états \(\vert x \rangle\). Remarquez que l’état de superposition uniforme a une amplitude de probabilité sur l’état marqué égale à \(\sqrt{\epsilon} = \frac{1}{\sqrt{2^n}}\). C’est bien plus que la probabilité \(\epsilon = \frac{1}{2^n}\) de choisir l’état marqué lors d’un tirage uniforme. Cette observation est vraie avant même d’avoir utilisé une seule fois l’oracle quantique \(U_f\). C’est une conséquence “gratuite” du fait que les états quantiques sont décrits par des amplitudes de probabilité qui sont des racines carrées de probabilité.

Néanmoins cet avantage de départ de l’état quantique de superposition uniforme sur l’état probabiliste uniformément distribué (tirage aléatoire) ne fait pas tout. Il s’agit maintenant de trouver un moyen d’amplifier l’amplitude de probabilité de l’état marqué de l’ordre de \(\sqrt{\epsilon}\) à chaque fois qu’on applique l’oracle quantique \(U_f\). Si on arrive à faire ça, on aura un algorithme quantique d’amplification d’amplitude qui fournit une accélération quadratique par rapport au meilleur algorithme classique pour le problème de recherche non structurée. En effet on a vu qu’à chaque application de la fonction \(f\), un algorithme classique augmente la probabilité de trouver l’état marqué d’environ \(\epsilon\). En 1997, Lov Grover a réalisé cet exploit : il propose un algorithme quantique qui amplifie l’amplitude de probabilité de l’état marqué d’environ \(\sqrt{\epsilon}\) à chaque application de l’oracle quantique \(U_f\).

L’algorithme d’amplification d’amplitude de Grover

Pour comprendre les détails de l’algorithme de Grover, il est très utile d’avoir bien compris comment transformer l’oracle à qubit auxiliaire \(U_f\) en l’oracle à phase associé. L’oracle à phase \(\tilde{U}_f\) est une réflexion par rapport à l’état marqué. On utilise également une réflexion \(R_s\) par rapport à l’état de superposition uniforme \(\vert s \rangle\). En effet on a vu que l’angle \(\theta\) entre l’état marqué et l’état de superposition uniforme est de l’ordre de \(\sqrt{\epsilon}\). Comme la composition de deux réflexions entre deux droites formant un angle \(\theta\) est une rotation d’angle \(2 \theta\), on obtient ainsi une rotation d’angle de l’ordre de \(\sqrt{\epsilon}\) dans le plan défini par l’état de superposition uniforme et l’état marqué. En appliquant cette rotation de l’ordre de \(\frac{1}{\sqrt{\epsilon}} = \sqrt{2^n}\) fois, on parvient à transformer l’état de superposition uniforme en l’état marqué. Il s’agit d’une accélération quadratique par rapport au meilleur algorithme classique. Cette accélération quadratique peut faire une différence importante : si par exemple \(n=20\), on peut trouver l’état marqué en faisant environ 1 000 000 d’appels à la fonction classique \(f\) tandis qu’environ 1 000 appels à l’oracle quantique \(U_f\) suffisent.

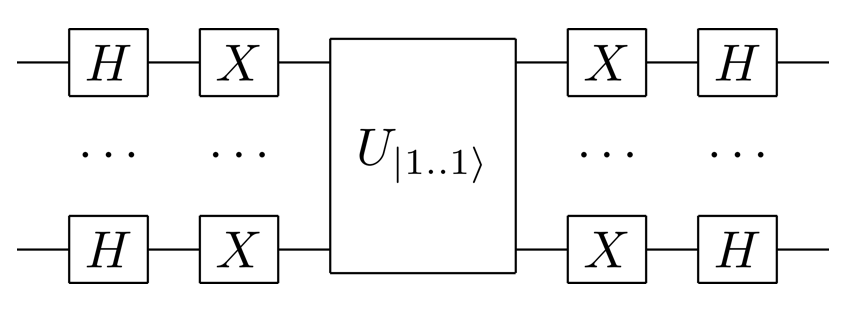
Pour pouvoir décrire l’algorithme d’amplification d’amplitude de Grover, il ne me reste plus qu’à donner l’opération quantique qui permet de réaliser une réflexion par rapport à l’état de superposition uniforme :

On peut remarquer que cette opération est construite à partir de \(U_{\vert 1 .. 1 \rangle}\), la réflexion par rapport à l’état “tout 1” : \(\vert 1 .. 1 \rangle\). Plus précisément, on conjugue \(U_{\vert 1 .. 1 \rangle}\) par une opération qui transforme l’état de superposition uniforme \(\vert s \rangle\) en l’état \(\vert 1 .. 1 \rangle\). Appliquer une porte \(H\) à chaque qubit puis une porte \(X\) à chaque qubit fournit cette opération. Ce billet de blog explique la technique de conjugaison, très courante en algorithmique quantique, et donne différentes façons d’implémenter \(U_{\vert 1 .. 1 \rangle}\).

Je peux maintenant décrire entièrement l’algorithme d’amplification d’amplitude de Grover. Il consiste à :

1. Préparer l’état quantique de superposition uniforme.
2. Appliquer de l’ordre de \(\sqrt{2^n}\) fois la suite d’opérations suivante:
   • réflexion par rapport à l’état marqué.
   • réflexion par rapport à l’état de superposition uniforme.
3. Mesurer tous les qubits.

En termes d’opérations quantiques, cela revient à :

1. Appliquer une porte \(H\) à chacun des \(n\) qubits d’input.
2. Appliquer de l’ordre de \(\sqrt{2^n}\) fois la suite d’opérations suivante:
   • appliquer \(\tilde{U}_f\).
   • appliquer une porte \(H\) puis une porte \(X\) à chaque qubit. Appliquer une réflexion par rapport à l’état “tout 1”. Appliquer une porte \(X\) puis une porte \(H\) à chaque qubit.
3. Mesurer tous les qubits.

Avec grande probabilité, on obtient comme résultat de mesure les \(n\) bits correspondants à l’état marqué. Le nombre d’appels fait à \(U_f\) est égal à seulement environ la racine carré du nombre d’appels qu’on aurait fait à \(f\) si on avait voulu trouver l’état marqué avec un ordinateur classique.

Conclusion

L’algorithme d’amplification d’amplitude de Grover fournit une accélération quantique quadratique par rapport au meilleur algorithme classique pour la recherche non structurée.

La plupart des problèmes de recherche qu’on rencontre en pratique ont une structure : savoir qu’un élément n’est pas marqué peut impliquer qu’un autre élément n’est pas marqué non plus. Néanmoins il est courant qu’une sous-routine (une partie) d’un algorithme classique consiste à effectuer une recherche exhaustive pour trouver un élément marqué sans tenir compte de la structure du problème. Dans ces cas, il est possible de donner un algorithme quantique en “groverisant” l’algorithme classique : on garde le plan de l’algorithme classique mais on remplace les sous-routines de recherche exhaustive par l’amplification d’amplitude de Grover. Trouver un tel algorithme quantique demande de bien connaitre les différents algorithmes classiques permettant de résoudre un problème afin de réussir à appliquer l’amplification d’amplitude de Grover au bon endroit !

La découverte de nouveaux algorithmes quantiques par groverisation d’un algorithme classique est une approche très fructueuse. Néanmoins elle ne fournit jamais des accélérations quantiques meilleures que quadratiques puisque l’accélération quantique de l’amplification d’amplitude est elle-même quadratique.